Robust passive dynamics of the musculoskeletal system compensate for unexpected surface changes during human hopping

Abstract

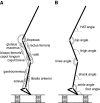
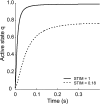
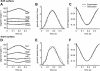
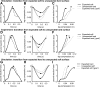
When human hoppers are surprised by a change in surface stiffness, they adapt almost instantly by changing leg stiffness, implying that neural feedback is not necessary. The goal of this simulation study was first to investigate whether leg stiffness can change without neural control adjustment when landing on an unexpected hard or unexpected compliant (soft) surface, and second to determine what underlying mechanisms are responsible for this change in leg stiffness. The muscle stimulation pattern of a forward dynamic musculoskeletal model was optimized to make the model match experimental hopping kinematics on hard and soft surfaces. Next, only surface stiffness was changed to determine how the mechanical interaction of the musculoskeletal model with the unexpected surface affected leg stiffness. It was found that leg stiffness adapted passively to both unexpected surfaces. On the unexpected hard surface, leg stiffness was lower than on the soft surface, resulting in close-to-normal center of mass displacement. This reduction in leg stiffness was a result of reduced joint stiffness caused by lower effective muscle stiffness. Faster flexion of the joints due to the interaction with the hard surface led to larger changes in muscle length, while the prescribed increase in active state and resulting muscle force remained nearly constant in time. Opposite effects were found on the unexpected soft surface, demonstrating the bidirectional stabilizing properties of passive dynamics. These passive adaptations to unexpected surfaces may be critical when negotiating disturbances during locomotion across variable terrain.

Fig. 1.

A: schematic representation of the musculoskeletal model used in this study. B: definition of joint and segment angles. HAT, head-arm-trunk segment.

Fig. 2.

Active state q vs. time. At time 0, STIM (stimulation of nine muscles of the lower extremity) changes from 0 to either 1 or 0.18. Note that, when STIM is 0.18, the active state q rises slower than when STIM is 1 and reaches a steady state of ∼0.8.

Fig. 3.

Time histories of segment angles with respect to the horizontal (A and D), ground reaction force normalized to body weight (B and E), and center of mass (COM) displacement (C and F). Experimental data are derived from hops of one representative subject, with a low-pass filtering of the marker data at 7 Hz (24). Simulation data are derived by optimizing muscle stimulation STIM(t) to make the model match the experimental data, separately for a soft (A–C) and a hard surface (D–F).

Fig. 4.

Time histories from touch down to toe-off of ground reaction force normalized to body weight (A, D, and G) and leg compression (B, E, and H). C, F, and I: ground reaction force vs. leg compression, plotted from touch down to midstance. D, E, and F: for comparison, experimental data are shown from Fig. 7A of Moritz and Farley (24). No experimental data were available on unexpected soft surfaces. •, Midstance.

Fig. 5.

Time histories from touch down to toe-off of surface compression (A and D), leg compression (B and E) (similar to Fig. 4, B and E), and COM displacement (C and F).

Fig. 6.

Time histories from touch down to toe-off of joint angles (A and F), ankle moment vs. ankle angle change from touch down to midstance (B and G), and muscle force vs. muscle-tendon complex (MTC) length change for m. soleus (SO; C and H), m. gastrocnemius (GA; D and I), and m. tibialis anterior (TA; E and J). Arrows indicate the progression in time.

Fig. 7.

Time histories of m. soleus force (A), MTC length change (B), and muscle force vs. MTC length change (C). D: contractile element (CE) length normalized to optimal length. E: CE velocity. F: active state q vs. MTC length change of m. soleus. Data in D–F are plotted as a function of MTC length change to highlight the effect on effective muscle stiffness shown in C. Force-length (G) and force-velocity (H) relationships for the active states q indicated in F are shown. These correspond to an MTC length change of 0.012 m relative to touch down. The effects of changes in CE length (Δlce) and CE velocity (Δvce) on muscle force are indicated along the force-length and force-velocity curves, whereas the effect of change in q (Δq) on muscle force is indicated by the height of the curve. Note that force rise as shown in C mainly depends on the rise in q (F).