Morphometric integration and modularity in configurations of landmarks: tools for evaluating a priori hypotheses

Abstract

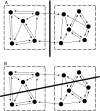
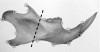
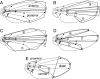
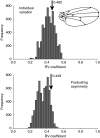
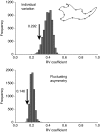
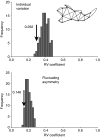
Identifying the modular components of a configuration of landmarks is an important task of morphometric analyses in evolutionary developmental biology. Modules are integrated internally by many interactions among their component parts, but are linked to one another only by few or weak interactions. Accordingly, traits within modules are tightly correlated with each other, but relatively independent of traits in other modules. Hypotheses concerning the boundaries of modules in a landmark configuration can therefore be tested by comparing the strength of covariation among alternative partitions of the configuration into subsets of landmarks. If a subdivision coincides with the true boundaries between modules, the correlations among subsets should be minimal. This article introduces Escoufier's RV coefficient and the multi-set RV coefficient as measures of the correlation between two or more subsets of landmarks. These measures can be compared between alternative partitions of the configuration into subsets. Because developmental interactions are tissue bound, it is sensible to require that modules should be spatially contiguous. I propose a criterion for spatial contiguity for sets of landmarks using an adjacency graph. The new methods are demonstrated with data on shape of the wing in Drosophila melanogaster and the mandible of the house mouse.

Fig. 1

Delimiting modules by comparing different partitions of the structure. Each diagram shows two modules (dashed lines) whose parts are integrated internally by many interactions (arrows), but which are relatively independent of each other because there are only few interactions between modules. The bold lines indicate two ways to partition the overall structure into two subsets. (A) The subdivision coincides with the boundary between modules. (B) The subdivision does not coincide with the modular boundary and therefore goes across both modules. Note that the dividing line in (B) intersects many more arrows than in (A). Accordingly, there are more interactions between the parts in the two subsets, and a stronger covariation between subsets is expected.

Fig. 2

Wing of Drosophila melanogaster with the landmarks used in the example (circles) and the approximate location of the boundary between the anterior and posterior developmental compartments (dashed line).

Fig. 3

A mouse mandible with the landmarks used in the analysis (circles). The dashed line indicates the boundary between the alveolar region (to the right) and the ascending ramus (to the left), which have been suggested as possible modules.

Fig. 4

Possible subdivisions of the Drosophila wing. (A) The anterior and posterior compartments. (B) The division into wing sectors according to intervein areas (Birdsall et al. 2000; Zimmerman et al. 2000; Palsson and Gibson 2004;). (C) The extended version of the division into three sectors, covering all 15 landmarks. Note that the sectors B and D are the same as the anterior and posterior compartments. (D) Division into three mutually exclusive wing sectors. (E) Division into proximal, central, and distal regions.

Fig. 5

Histograms of the squared trace correlations between all possible partitions of the Drosophila wing. The values of the squared trace correlation between the subsets of landmarks in the anterior and posterior compartments are indicated by arrows.

Fig. 6

Histograms of the squared trace correlations for all possible partitions of the mouse mandible. The trace correlations between the alveolar region and the ascending ramus (indicated by arrows) are the lowest values observed for any of the 6435 partitions of the configuration of 15 landmarks into subsets of seven and eight landmarks.

Fig. 7

Definition of spatial contiguity for sets of landmarks. (A) An adjacency graph for the Drosophila wing. The edges of this graph connect neighboring landmarks. This adjacency graph has been obtained as the Delaunay triangulation (e.g., de Berg et al. 2000) of the landmark positions in the mean shape. A set of landmarks is said to be contiguous if every one of its landmarks is connected directly or indirectly to all other landmarks of the set by the edges of this graph. (B) An example of a contiguous set of landmarks (black circles). Within this set, all landmarks are connected to each other either directly or indirectly via other landmarks of the set. (C) An example of a set of landmarks that is not contiguous. It consists of one group of three landmarks at the base of the wing and another group near the wing tip (solid black circles), which are separated from each other by landmarks belonging to the other set (open circles).

Fig. 8

Possible problems with the Delaunay triangulations for configurations with a complex outline. The outline of the mouse mandible is indented in regions such as the space between the incisor and molar teeth or between the muscle attachment processes. Some of the edges of the Delaunay triangulation are therefore outside the contour of the mandible (dashed lines). These may be omitted for the consideration of spatial contiguity. For each quadrilateral of neighboring landmarks, the Delaunay triangulation contains just one of the two diagonals; the second diagonal may be added to the adjacency graph (dot-dashed lines; note that this has not been done for all possible quadrilaterals).

Fig. 9

Histograms of the squared trace correlations for those partitions of the Drosophila wing that produced spatially contiguous subsets of landmarks. The values of the squared trace correlation between the subsets of landmarks in the anterior and posterior compartments are indicated by arrows.

Fig. 10

Histograms of the RV coefficients for those partitions of the mouse mandible that produced spatially contiguous subsets of landmarks. The values of the RV coefficients between the subsets of landmarks in the alveolar region and ascending ramus are indicated by arrows.