Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2009 Jun;36(6):2258-68.
doi: 10.1118/1.3130047.

Scatter correction for cone-beam CT in radiation therapy

Lei Zhu  1 , Yaoqin Xie, Jing Wang, Lei Xing
Affiliations

Scatter correction for cone-beam CT in radiation therapy

Lei Zhu et al. Med Phys. 2009 Jun.

Abstract

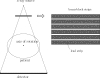
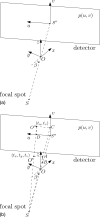
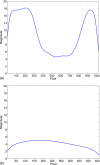
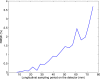
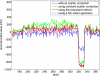
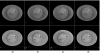
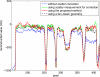
Cone-beam CT (CBCT) is being increasingly used in modern radiation therapy for patient setup and adaptive replanning. However, due to the large volume of x-ray illumination, scatter becomes a rather serious problem and is considered as one of the fundamental limitations of CBCT image quality. Many scatter correction algorithms have been proposed in literature, while a standard practical solution still remains elusive. In radiation therapy, the same patient is scanned repetitively during a course of treatment, a natural question to ask is whether one can obtain the scatter distribution on the first day of treatment and then use the data for scatter correction in the subsequent scans on different days. To realize this scatter removal scheme, two technical pieces must be in place: (i) A strategy to obtain the scatter distribution in on-board CBCT imaging and (ii) a method to spatially match a prior scatter distribution with the on-treatment CBCT projection data for scatter subtraction. In this work, simple solutions to the two problems are provided. A partially blocked CBCT is used to extract the scatter distribution. The x-ray beam blocker has a strip pattern, such that partial volume can still be accurately reconstructed and the whole-field scatter distribution can be estimated from the detected signals in the shadow regions using interpolation/extrapolation. In the subsequent scans, the patient transformation is determined using a rigid registration of the conventional CBCT and the prior partial CBCT. From the derived patient transformation, the measured scatter is then modified to adapt the new on-treatment patient geometry for scatter correction. The proposed method is evaluated using physical experiments on a clinical CBCT system. On the Catphan 600 phantom, the errors in Hounsfield unit (HU) in the selected regions of interest are reduced from about 350 to below 50 HU; on an anthropomorphic phantom, the error is reduced from 15.7% to 5.4%. The proposed method is attractive in applications where a high CBCT image quality is critical, for example, dose calculation in adaptive radiation therapy.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Work flow of the scatter correction using prior scatter measurement from partially blocked CBCT.
Figure 2
Figure 2
Geometry of the partially blocked CBCT system.
Figure 3
Figure 3
The cone-beam projection geometry and coordinate systems. (a) coordinate systerm before transformation; (b) coordinate system after the object translates by tx,ty,tz in the directions of the x, y, and z axes, respectively.
Figure 4
Figure 4
MC simulation on the Zubal phantom.
Figure 5
Figure 5
1D profiles of the scatter distribution shown in Fig. 4. Note that the same scale is used in both plots. (a) Central horizontal profile; (b) Central vertical profile.
Figure 6
Figure 6
Relationship between the scatter estimation error and the sampling period based on the MC simulation.
Figure 7
Figure 7
Axial views of the reconstructed Catphan©600 phantom. Display window: [−500 500] HU. In the regular scan after partial CBCT, the object is translated (ty=10 mm, tz=10 mm): (a) No scatter correction; (b) using constant scatter correction; (c) scatter corrected using the proposed method; and (d) scatter corrected using the measured scatter from the partial CBCT, but without using the “registration” algorithm as defined in Eq. 5. The white arrow indicates the image distortion.
Figure 8
Figure 8
Reconstruction of the Catphan©600 phantom using a narrow collimator (a fan-beam geometry).
Figure 9
Figure 9
Comparison of 1D profiles in Figs. 78 passing through one contrast rod. The data on the body annulus are excluded.
Figure 10
Figure 10
Axial views of the reconstructed Catphan©600 phantom with different transformations in the second regular CBCT scan. Display window: [−500 500] HU. Upper row: Without scatter correction; bottom row: Using the proposed method: (a) No transformation; (b) ty=10 mm; (c) ty=20 mm; and (d) ty=5 mm, γx=3°. The transformation parameters (tx,y,z and γx,y,z) are zeros unless otherwise specified.
Figure 11
Figure 11
Projection image of partially blocked CBCT and the corresponding measured scatter distribution.
Figure 12
Figure 12
CB projection image and its scatter estimate using the proposed method.
Figure 13
Figure 13
Axial views of the reconstructed anthropomorphic phantom. Display window: [−800 450] HU. In the regular scan after partial CBCT, the phantom is transformed by parameters of tx=−4.0 mm, ty=8.4 mm, tz=−2.2 mm, and γx=2.01°, γy=1.99°, γz=0.55°: (a) No scatter correction; (b) measurement-based scatter correction using a partially blocked CBCT as a prescan; (c) scatter corrected using the proposed method; and (d) using a narrow collimator (a fan-beam equivalent geometry). The line in (a) indicates the location where the 1D profiles shown in Fig. 14 are taken.
Figure 14
Figure 14
Comparison of 1D vertical profiles in Fig. 13.
Figure 15
Figure 15
Sagittal and coronal views of the reconstructed anthropomorphic phantom. Display window: [−800 450] HU: (a) No scatter correction and (b) scatter corrected using the proposed method.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Fox T. R., Nisius D. T., Aradate H., and Saito Y., “Practical x-ray scatter measurements for volume CT detector design,” in Medical Imaging 2001: Physics of Medical Imaging, edited by Antonuk Larry E. and Yaffe Martin J.
    2. [Proc. SPIE PSISDG 4320, 808–814 (2009)].
    1. de la Zerda A., Armbruster B., and Xing L., “Formulating adaptive radiation therapy (ART) treatment planning into a closed-loop control framework,” Phys. Med. Biol. PHMBA7 52(14), 4137–4153 (2007).10.1088/0031-9155/52/14/008 - DOI - PubMed
    1. Lee L., Le Q.-T., and Xing L., “Retrospective IMRT dose reconstruction based on cone-beam ct and mlc log-file,” Int. J. Radiat. Oncol., Biol., Phys. IOBPD3 70(2), 634–644 (2008). - PubMed
    1. van Zijtveld M., Dirkx M., and Heijmen B., “Correction of cone beam CT values using a planning CT for derivation of the ‘dose of the day’,” Radiother. Oncol. RAONDT 85(2), 195–200 (2007).10.1016/j.radonc.2007.08.010 - DOI - PubMed
    1. Siewerdsen J. H., Daly M. J., Bakhtiar B., Moseley D. J., Richard S., Keller H., and Jaffray D. A., “A simple, direct method for x-ray scatter estimation and correction in digital radiography and cone-beam CT,” Med. Phys. MPHYA6 33(1), 187–197 (2006).10.1118/1.2148916 - DOI - PubMed

Publication types

LinkOut - more resources