The behavioral economics of choice and interval timing
- PMID: 19618985
- PMCID: PMC2743419
- DOI: 10.1037/a0016171
The behavioral economics of choice and interval timing
Abstract
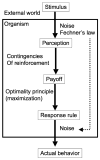
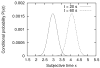
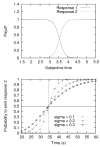
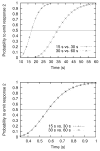
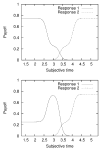
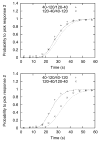
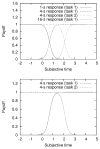
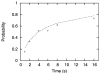
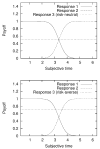
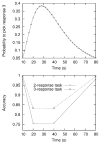
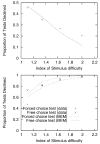
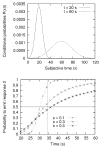
The authors propose a simple behavioral economic model (BEM) describing how reinforcement and interval timing interact. The model assumes a Weber-law-compliant logarithmic representation of time. Associated with each represented time value are the payoffs that have been obtained for each possible response. At a given real time, the response with the highest payoff is emitted. The model accounts for a wide range of data from procedures such as simple bisection, metacognition in animals, economic effects in free-operant psychophysical procedures, and paradoxical choice in double-bisection procedures. Although it assumes logarithmic time representation, it can also account for data from the time-left procedure usually cited in support of linear time representation. It encounters some difficulties in complex free-operant choice procedures, such as concurrent mixed fixed-interval schedules as well as some of the data on double bisection, which may involve additional processes. Overall, BEM provides a theoretical framework for understanding how reinforcement and interval timing work together to determine choice between temporally differentiated reinforcers.
Copyright (c) 2009 APA, all rights reserved.
Figures


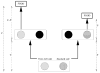
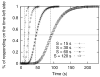
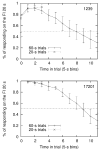
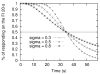
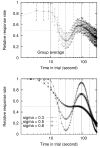
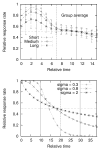
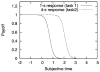
Similar articles
-
Timing, learning, and forgetting.Ann N Y Acad Sci. 1984;423:346-60. doi: 10.1111/j.1749-6632.1984.tb23443.x. Ann N Y Acad Sci. 1984. PMID: 6588799
-
A tuned-trace theory of interval-timing dynamics.J Exp Anal Behav. 2002 Jan;77(1):105-24. doi: 10.1901/jeab.2002.77-105. J Exp Anal Behav. 2002. PMID: 11859841 Free PMC article.
-
Effects of free food deliveries and temporal contiguity on choice under concurrent-chain schedules.Psychon Bull Rev. 2009 Aug;16(4):736-41. doi: 10.3758/PBR.16.4.736. Psychon Bull Rev. 2009. PMID: 19648461
-
Operant conditioning.Annu Rev Psychol. 2003;54:115-44. doi: 10.1146/annurev.psych.54.101601.145124. Epub 2002 Jun 10. Annu Rev Psychol. 2003. PMID: 12415075 Free PMC article. Review.
-
Time and memory: towards a pacemaker-free theory of interval timing.J Exp Anal Behav. 1999 Mar;71(2):215-51. doi: 10.1901/jeab.1999.71-215. J Exp Anal Behav. 1999. PMID: 10220931 Free PMC article. Review.
Cited by
-
Evaluating information-seeking approaches to metacognition.Curr Zool. 2011;57(4):531-542. doi: 10.1093/czoolo/57.4.531. Curr Zool. 2011. PMID: 26779256 Free PMC article.
-
"Play it Again": a new method for testing metacognition in animals.Anim Cogn. 2012 Mar;15(2):187-99. doi: 10.1007/s10071-011-0445-y. Epub 2011 Sep 11. Anim Cogn. 2012. PMID: 21909935 Free PMC article.
-
Interactions of timing and prediction error learning.Behav Processes. 2014 Jan;101:135-45. doi: 10.1016/j.beproc.2013.08.005. Epub 2013 Aug 17. Behav Processes. 2014. PMID: 23962670 Free PMC article. Review.
-
Everywhere and everything: The power and ubiquity of time.Int J Comp Psychol. 2015;28:http://escholarship.org/uc/item/8hg831n3. Int J Comp Psychol. 2015. PMID: 28392622 Free PMC article.
-
Theoretical implications of quantitative properties of interval timing and probability estimation in mouse and rat.J Exp Anal Behav. 2017 Jul;108(1):39-72. doi: 10.1002/jeab.261. Epub 2017 Jun 27. J Exp Anal Behav. 2017. PMID: 28653484 Free PMC article.
References
-
- Ainslie G, Monterosso L. A marketplace in the brain? Science. 2004;306:421–423. - PubMed
-
- Bizo LA, Chu JYM, Sanabria F, Killeen PR. The failure of Weber’s law in time perception and production. Behavioural Processes. 2006;71:201–210. - PubMed
-
- Bizo LA, White KG. Pacemaker rate in the behavioral theory of timing. Journal of Experimental Psychology: Animal Behavior Processes. 1994b;20:308–321.

