Solving a Hamiltonian Path Problem with a bacterial computer

Abstract

Background: The Hamiltonian Path Problem asks whether there is a route in a directed graph from a beginning node to an ending node, visiting each node exactly once. The Hamiltonian Path Problem is NP complete, achieving surprising computational complexity with modest increases in size. This challenge has inspired researchers to broaden the definition of a computer. DNA computers have been developed that solve NP complete problems. Bacterial computers can be programmed by constructing genetic circuits to execute an algorithm that is responsive to the environment and whose result can be observed. Each bacterium can examine a solution to a mathematical problem and billions of them can explore billions of possible solutions. Bacterial computers can be automated, made responsive to selection, and reproduce themselves so that more processing capacity is applied to problems over time.

Results: We programmed bacteria with a genetic circuit that enables them to evaluate all possible paths in a directed graph in order to find a Hamiltonian path. We encoded a three node directed graph as DNA segments that were autonomously shuffled randomly inside bacteria by a Hin/hixC recombination system we previously adapted from Salmonella typhimurium for use in Escherichia coli. We represented nodes in the graph as linked halves of two different genes encoding red or green fluorescent proteins. Bacterial populations displayed phenotypes that reflected random ordering of edges in the graph. Individual bacterial clones that found a Hamiltonian path reported their success by fluorescing both red and green, resulting in yellow colonies. We used DNA sequencing to verify that the yellow phenotype resulted from genotypes that represented Hamiltonian path solutions, demonstrating that our bacterial computer functioned as expected.

Conclusion: We successfully designed, constructed, and tested a bacterial computer capable of finding a Hamiltonian path in a three node directed graph. This proof-of-concept experiment demonstrates that bacterial computing is a new way to address NP-complete problems using the inherent advantages of genetic systems. The results of our experiments also validate synthetic biology as a valuable approach to biological engineering. We designed and constructed basic parts, devices, and systems using synthetic biology principles of standardization and abstraction.

Figure 1

A directed graph containing a unique Hamiltonian path. The seven nodes are connected with fourteen directed edges. The Hamiltonian Path Problem is to start at node 1, end at node 5, and visit each node exactly once while following the available edges. Adleman programmed a DNA computer to find the unique Hamiltonian path in this graph (1→4→7→2→3→6→5).

Figure 2

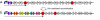
Illustration of the use of split genes to encode a seven node Hamiltonian Path Problem. a. The manner in which each of the directed edges in Figure 1 could be encoded in DNA is illustrated. The 5' half of each node gene is denoted by and the 3' half is denoted by . DNA edges are depicted by gene halves connected by arrows and flanked by triangles that represent hixC sites. Transcription in the direction of the solid arrow would terminate early and result in the expression of only one marker gene. b. Hin-mediated recombination would randomly reshuffle the DNA edges into many configurations. One possible example of an HPP solution configuration with its marker gene halves reunited is illustrated. Transcription in the direction of the solid arrow would result in expression of the six marker gene phenotypes.

Figure 3

Markov Chain model of solving a Hamiltonian Path Problem. Each colored line represents a different starting configuration of a graph with four nodes and three edges. As the number of flips increases, the probability of finding a Hamiltonian path solution converges to 1/48, or about 0.02.

Figure 4

DNA constructs that encode a three node Hamiltonian Path Problem. a. The three node directed graph contains a Hamiltonian path starting at the RFP node, proceeding to the GFP node, and finishing at the TT node. b. Construct ABC represents a solution to the three node HPP. Its three hixC-flanked DNA segments are in the proper order and orientation for the GFP and RFP genes to be intact. ACB has the RFP gene intact but not the GFP gene, while BAC has neither gene intact.

Figure 5

Detecting solutions to a Hamiltonian Path Problem with bacterial computing. Bacterial colonies containing each of the three starting constructs ABC, ACB, and BAC are shown on the left. Hin recombination resulted in the three plates of colonies on the right. The callouts include yellow colored colonies that contain solutions to the HPP.

Figure 6

DNA sequence verification of HPP solutions. Three yellow fluorescent colonies from each of the three recombination plates were used for plasmid preparation and DNA sequencing. The number of ABC and ABC' solution genotypes found for each of the starting constructs is listed. The order and orientations of GFP (green) and RFP (red) gene halves for each of the starting constructs and solutions is illustrated.

Figure 7

Clones isolated from HPP recombination plates. Selected colonies from ABC, ACB, and BAC recombination plates were grown overnight and replated. The results emphasize the diversity of colors produced by the bacterial computer in the HPP experiment.