Automated voxel-based 3D cortical thickness measurement in a combined Lagrangian-Eulerian PDE approach using partial volume maps
- PMID: 19648050
- PMCID: PMC3068613
- DOI: 10.1016/j.media.2009.07.003
Automated voxel-based 3D cortical thickness measurement in a combined Lagrangian-Eulerian PDE approach using partial volume maps
Abstract
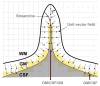
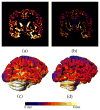
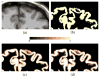
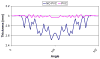
Accurate cortical thickness estimation is important for the study of many neurodegenerative diseases. Many approaches have been previously proposed, which can be broadly categorised as mesh-based and voxel-based. While the mesh-based approaches can potentially achieve subvoxel resolution, they usually lack the computational efficiency needed for clinical applications and large database studies. In contrast, voxel-based approaches, are computationally efficient, but lack accuracy. The aim of this paper is to propose a novel voxel-based method based upon the Laplacian definition of thickness that is both accurate and computationally efficient. A framework was developed to estimate and integrate the partial volume information within the thickness estimation process. Firstly, in a Lagrangian step, the boundaries are initialized using the partial volume information. Subsequently, in an Eulerian step, a pair of partial differential equations are solved on the remaining voxels to finally compute the thickness. Using partial volume information significantly improved the accuracy of the thickness estimation on synthetic phantoms, and improved reproducibility on real data. Significant differences in the hippocampus and temporal lobe between healthy controls (NC), mild cognitive impaired (MCI) and Alzheimer's disease (AD) patients were found on clinical data from the ADNI database. We compared our method in terms of precision, computational speed and statistical power against the Eulerian approach. With a slight increase in computation time, accuracy and precision were greatly improved. Power analysis demonstrated the ability of our method to yield statistically significant results when comparing AD and NC. Overall, with our method the number of samples is reduced by 25% to find significant differences between the two groups.
Figures










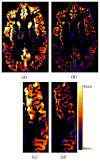
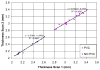


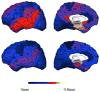



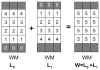

References
-
- Besag J. On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society. 1986;48:259–302.
-
- Collins D, Zijdenbos A, Kollokian V, Sled J, Kabani N, Holmes C, Evans A. Design and construction of a realistic digital brain phantom. IEEE Transactions on Medical Imaging. 1998;17 (3):463–468. - PubMed
-
- Dale A, Fischl B, Sereno M. Cortical surface-based analysis I: segmentation and surface reconstruction. NeuroImage. 1999;9 (2):179–194. - PubMed
-
- Diep T-M, Bourgeat P, Ourselin S. Efficient use of cerebral cortical thickness to correct brain MR segmentation. IEEE International Symposium on Biomedical Imaging (ISBI’07). IEEE; Washington, DC, USA. 2007. pp. 592–595.
-
- Faul F, Erdfelder E, Lang AG, Buchner A. G* power 3: a flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods. 2007;39 (2):175–191. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

