Optimal drug combinations and minimal hitting sets
- PMID: 19660129
- PMCID: PMC2738654
- DOI: 10.1186/1752-0509-3-81
Optimal drug combinations and minimal hitting sets
Abstract
Background: Identifying effective drug combinations that significantly improve over single agents is a challenging problem. Pairwise combinations already represent a huge screening effort. Beyond two drug combinations the task seems unfeasible.
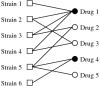
Results: In this work we introduce a method to uncover drug combinations with a putative effective response when presented to a heterogeneous population of malignant agents (strains), such as cancer cell lines or viruses. Using data quantifying the effect of single drugs over several individual strains, we search for minimal drug combinations that successfully target all strains. We show that the latter problem can be mapped to a minimal hitting set problem in mathematics. We illustrate this approach using data for the NCI60 panel of tumor derived cell lines, uncovering 14 anticancer drug combinations.
Conclusion: The drug-response graph and the associated minimal hitting set method can be used to uncover effective drug combinations in anticancer drug screens and drug development programs targeting heterogeneous populations of infectious agents such as HIV.
Figures

References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

