Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Aug;34(3-4):301-14.
doi: 10.1007/s10867-008-9081-4. Epub 2008 Jul 18.

Feedback suppression of neural synchrony in two interacting populations by vanishing stimulation

Natalia Tukhlina  1 , Michael Rosenblum
Affiliations

Feedback suppression of neural synchrony in two interacting populations by vanishing stimulation

Natalia Tukhlina et al. J Biol Phys. 2008 Aug.

Abstract

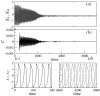
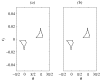
We discuss the suppression of collective synchrony in a system of two interacting oscillatory networks. It is assumed that the first network can be affected by the stimulation, whereas the activity of the second one can be monitored. The study is motivated by ongoing attempts to develop efficient techniques for the manipulation of pathological brain rhythms. The suppression mechanism we consider is related to the classical problem of interaction of active and passive systems. The main idea is to connect a specially designed linear oscillator to the active system to be controlled. We demonstrate that the feedback loop, organized in this way, provides an efficient suppression. We support the discussion of our approach by a theoretical treatment of model equations for the collective modes of both networks, as well as by the numerical simulation of two coupled populations of neurons. The main advantage of our approach is that it provides a vanishing-stimulation control, i.e., the stimulation reduces to the noise level as soon as the goal is achieved.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
a The evolution of the mean field of a population of 500 Bonhoeffer–van der Pol neurons (1) for subcritical coupling ε = 0.01 (bold line) and supercritical coupling ε = 0.03 (solid line). b Transition to the macroscopic mean field in the model (1)
Fig. 2
Fig. 2
Suggested suppression scheme. The LFP of the population B is measured by the recording electrode and is fed back via the field application electrode to the population A. The feedback loop contains a passive oscillator playing the role of a band pass filter, an integrator, a summator, and two amplifiers
Fig. 3
Fig. 3
Stability domains (areas inside closed curves) for the controlled model system (7) for the case of identical (a) and nonidentical (b) subpopulations. c The case when the population B, where the measurement is performed, is stable (ξ2 = − 0.02). The other parameters are: ε = 0.05, α = 0.3ω0, μ = 500, and β = 0. Note that stability of the fixed point A = B = 0 corresponds to the asynchronous dynamics of the oscillator ensemble. Instability of the fixed point corresponds to synchronous ensemble dynamics with nonzero mean field
Fig. 4
Fig. 4
Suppression of synchrony in two coupled Bonhoeffer–van der Pol subpopulations (11). a The mean fields of these subpopulations (XA, XB) without (t < 500) and with (t > 500) an external feedback. b The control signal formula image vs time. Synchronous (c) and asynchronous (d) dynamics of two neurons in the absence and in the presence of the stimulation, respectively
Fig. 5
Fig. 5
Domains of suppression for two coupled Bonhoeffer–van der Pol ensembles (11). Each population consists of N = 500 oscillators. The suppression factor is shown in a color scale coding: for population A (a) and B (b)
Fig. 6
Fig. 6
Domains of suppression for two coupled Bonhoeffer–van der Pol ensembles (11). Each population consists of N = 500 oscillators. The suppression factor is shown in color coding: a the suppression factor SA of the stimulated population A, b the suppression factor SB of the measured population B
Fig. 7
Fig. 7
Results of numerical analysis of the stability domains of the two coupled Bonhoeffer–van der Pol ensembles (11). The case of two coupled active populations is presented here: a the stimulated population A, b the monitored population B
Fig. 8
Fig. 8
Results of numerical analysis of the stability domains of the two coupled Bonhoeffer–van der Pol ensembles (11). a The stimulated population A is active, b the monitored population B is passive
See this image and copyright information in PMC

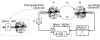
References

    1. None
    2. Tass, P.A.: Phase Resetting in Medicine and Biology. Stochastic Modelling and Data Analysis. Springer, Berlin (1999)
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1126/science.1099745', 'is_inner': False, 'url': 'https://doi.org/10.1126/science.1099745'}, {'type': 'PubMed', 'value': '15218136', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/15218136/'}]}
    2. Buzsáki, G., Draguhn, A.: Neuronal oscillations in cortical networks. Science 304, 1926–1929 (2004) - PubMed
    1. None
    2. Milton, J., Jung, P. (eds.): Epilepsy as a Dynamic Disease. Springer, Berlin (2003)
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1016/S0166-2236(97)01151-X', 'is_inner': False, 'url': 'https://doi.org/10.1016/s0166-2236(97)01151-x'}, {'type': 'PubMed', 'value': '9464684', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/9464684/'}]}
    2. Bergman, H., Feingold, A., Nini, A., Raz, A., Slovin, H., Abeles, M., Vaadia, E.: Physiological aspects of information processing in the basal ganglia of normal and parkinsonian primates. Trends Neurosci. 21, 32 (1998) - PubMed
    1. None
    2. Sarnthein, J., Morel, A., von Stein, A., Jeanmonod, D.: Thalamic theta field potentials and EEG: High thalamocortical coherence in patients with neurogenic pain, epilepsy and movement disorders. Thalamus & Related Systems 2, 321 (2003)