Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Aug;34(3-4):315-23.
doi: 10.1007/s10867-008-9077-0. Epub 2008 Jul 5.

Identifying complex brain networks using penalized regression methods

Eduardo Martínez-Montes  1 , Mayrim Vega-Hernández, José M Sánchez-Bornot, Pedro A Valdés-Sosa
Affiliations

Identifying complex brain networks using penalized regression methods

Eduardo Martínez-Montes et al. J Biol Phys. 2008 Aug.

Abstract

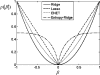
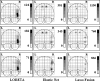
The recorded electrical activity of complex brain networks through the EEG reflects their intrinsic spatial, temporal and spectral properties. In this work we study the application of new penalized regression methods to i) the spatial characterization of the brain networks associated with the identification of faces and ii) the PARAFAC analysis of resting-state EEG. The use of appropriate constraints through non-convex penalties allowed three types of inverse solutions (Loreta, Lasso Fusion and ENet L) to spatially localize networks in agreement with previous studies with fMRI. Furthermore, we propose a new penalty based in the Information Entropy for the constrained PARAFAC analysis of resting EEG that allowed the identification in time, frequency and space of those brain networks with minimum spectral entropy. This study is an initial attempt to explicitly include complexity descriptors as a constraint in multilinear EEG analysis.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Penalty functions: Ridge (solid), Lasso (dash), ENet (dot), Entropy–Ridge (dot-dash)
Fig. 2
Fig. 2
Hotelling’s T2 images of sources of evoked N170 peak corresponding to topographic maps of correct face detection (upper panel), incorrect face detection (middle panel), and the difference between correct and incorrect detection (bottom panel)
Fig. 3
Fig. 3
Spectral signatures found by: a) unconstrained PARAFAC, b) PARAFAC with MPLS using a Ridge penalty. Components are identified as alpha (solid), theta (dash) and gamma (dot-dash)
Fig. 4
Fig. 4
Spectral signatures found by: a) PARAFAC with MPLS using ENet penalty, b) PARAFAC with MPLS using Entropy–Ridge penalty. Components are identified as alpha (solid), theta (dash) and gamma (dot-dash)
See this image and copyright information in PMC

References

    1. None
    2. Pascual-Marqui, R.D.: Review of methods for solving the EEG inverse problem. Int. J. Bioelectromagn. 1, (1), 75–86 (1999)
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1109/51.956819', 'is_inner': False, 'url': 'https://doi.org/10.1109/51.956819'}, {'type': 'PubMed', 'value': '11668896', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/11668896/'}]}
    2. Durka, P.J., Blinowska, K.J.: A unified time–frequency parametrization of EEG. IEEE Eng. Med. Biol. 20, (5), 47–53 (2001) - PubMed
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1126/science.1066168', 'is_inner': False, 'url': 'https://doi.org/10.1126/science.1066168'}, {'type': 'PubMed', 'value': '11809976', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/11809976/'}]}
    2. Makeig, S., Westerfield, M., Jung, T.P., Enghoff, S., Townsend, J., Courchesne, E., Sejnowski, T.J.: Dynamic brain sources of visual evoked responses. Science 295, 690–694 (2002) - PubMed
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1016/j.neuroimage.2004.03.039', 'is_inner': False, 'url': 'https://doi.org/10.1016/j.neuroimage.2004.03.039'}, {'type': 'PubMed', 'value': '15219576', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/15219576/'}]}
    2. Miwakeichi, F., Martínez-Montes, E., Valdés-Sosa, P.A., Nishiyama, N., Mizuhara, H., Yamaguchi, Y.: Decomposing EEG data into space–time–frequency components using Parallel Factor Analysis. Neuroimage 22, (3), 1035–1045 (2004) - PubMed
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1016/S1053-8119(03)00160-5', 'is_inner': False, 'url': 'https://doi.org/10.1016/s1053-8119(03)00160-5'}, {'type': 'PubMed', 'value': '12948704', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/12948704/'}]}
    2. Harrison, L., Penny, W.D., Friston, K.: Multivariate autoregressive modeling of fmri time series. Neuroimage 19, 1477–1491 (2003) - PubMed