Stochastic hierarchical systems: excitable dynamics

Abstract

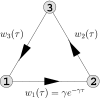
We present a discrete model of stochastic excitability by a low-dimensional set of delayed integral equations governing the probability in the rest state, the excited state, and the refractory state. The process is a random walk with discrete states and nonexponential waiting time distributions, which lead to the incorporation of memory kernels in the integral equations. We extend the equations of a single unit to the system of equations for an ensemble of globally coupled oscillators, derive the mean field equations, and investigate bifurcations of steady states. Conditions of destabilization are found, which imply oscillations of the mean fields in the stochastic ensemble. The relation between the mean field equations and the paradigmatic Kuramoto model is shown.

Fig. 1

Three-state model of a single excitable unit. State 1 denotes the rest state, followed by the excited or firing state 2. State 3 is the refractory state. The τs are the times elapsed after a state was entered. w_i(τ) defines the lifetimes in states i = 1,2,3, respectively

Fig. 2

Geometric sketch of the left and right hand side of (30). The star indicates the stationary solution considered in the text. Panels I and II show a saddle-node bifurcation. I two fixed points are created distinct from the already existing third fixed point, σ = 4.1. II One of the new fixed points merges with the old one, and both disappear, σ = 5.5. Panels III and IV show a pitchfork bifurcation. III the middle fixed point is given by the inflection point of the right-hand size of (30), σ = 3.6, D = 1.06·10^− 4. IV two new steady states are born from the middle one, σ = 4.4, D = 9·10^− 5. Other parameters: γ₀ = 0.05,τ₂ = 75,τ₃ = 260,ΔU₀ = 0.0005

Fig. 3

Surface of stationary solutions over the (σ,D)-plane

Fig. 4

Number of roots of (31) with positive real part in the γγ′-plane for different α. Solid line Hopf bifurcation. Dashed line saddle-node bifurcation

Fig. 5

Critical frequency at the Hopf bifurcation for different α as function of the rate

Fig. 6

Curves of the Hopf (solid) and saddle-node (dashed) bifurcations in σ,D-space. Numbers in the regions indicate the numbers of unstable eigenvalues for steady states

Fig. 7

Schematic bifurcation diagram: stationary values of P₂ for steady states and averaged values of P₂(t) for oscillatory states. sn_1,2 saddle-node bifurcations of steady states; H_1,2 Hopf bifurcations, T tangent bifurcation of oscillatory states

Fig. 8

Hopf bifurcation in the parameter plane of γ and γ′ and corresponding frequencies without delay (τ_D = 0) and with it (τ_D = 5)