Regression models of atlas appearance
- PMID: 19694260
- PMCID: PMC2807889
- DOI: 10.1007/978-3-642-02498-6_13
Regression models of atlas appearance
Abstract
Models of object appearance based on principal components analysis provide powerful and versatile tools in computer vision and medical image analysis. A major shortcoming is that they rely entirely on the training data to extract principal modes of appearance variation and ignore underlying variables (e.g., subject age, gender). This paper introduces an appearance modeling framework based instead on generalized multi-linear regression. The training of regression appearance models is controlled by independent variables. This makes it straightforward to create model instances for specific values of these variables, which is akin to model interpolation. We demonstrate the new framework by creating an appearance model of the human brain from MR images of 36 subjects. Instances of the model created for different ages are compared with average shape atlases created from age-matched sub-populations. Relative tissue volumes vs. age in models are also compared with tissue volumes vs. subject age in the original images. In both experiments, we found excellent agreement between the regression models and the comparison data. We conclude that regression appearance models are a promising new technique for image analysis, with one potential application being the representation of a continuum of mutually consistent, age-specific atlases of the human brain.
Figures

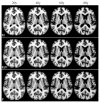

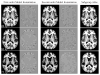


References
-
- Cootes TF, Taylor CJ, Cooper DH, Graham J. Active shape models – Their training and application. Comput Vision Image Understanding. 1995 Jan;61(1):38–59.
-
- Sozou P, Cootes T, Taylor C, Di-Mauro E. A non-linear generalisation of PDMs using polynomial regression. Proceedings of the Conference on British Machine Vision; Surrey, UK: BMVA Press; 1994. pp. 397–406.
-
- Davis BC, Fletcher PT, Bullitt E, Joshi S. Population shape regression from random design data. IEEE 11th International Conference on Computer Vision, ICCV; Oct. 2007; pp. 1–7.
-
- Holmes CJ, Hoge R, Collins L, Woods R, Toga AW, Evans AC. Enhancement of MR images using registration for signal averaging. J Comput Assist Tomogr. 1998 Mar;22(2):324–333. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
