Man bites mosquito: understanding the contribution of human movement to vector-borne disease dynamics
- PMID: 19707544
- PMCID: PMC2727792
- DOI: 10.1371/journal.pone.0006763
Man bites mosquito: understanding the contribution of human movement to vector-borne disease dynamics
Abstract
In metropolitan areas people travel frequently and extensively but often in highly structured commuting patterns. We investigate the role of this type of human movement in the epidemiology of vector-borne pathogens such as dengue. Analysis is based on a metapopulation model where mobile humans connect static mosquito subpopulations. We find that, due to frequency dependent biting, infection incidence in the human and mosquito populations is almost independent of the duration of contact. If the mosquito population is not uniformly distributed between patches the transmission potential of the pathogen at the metapopulation level, as summarized by the basic reproductive number, is determined by the size of the largest subpopulation and reduced by stronger connectivity. Global extinction of the pathogen is less likely when increased human movement enhances the rescue effect but, in contrast to classical theory, it is not minimized at an intermediate level of connectivity. We conclude that hubs and reservoirs of infection can be places people visit frequently but briefly and the relative importance of human and mosquito populations in maintaining the pathogen depends on the distribution of the mosquito population and the variability in human travel patterns. These results offer an insight in to the paradoxical observation of resurgent urban vector-borne disease despite increased investment in vector control and suggest that successful public health intervention may require a dual approach. Prospective studies can be used to identify areas with large mosquito populations that are also visited by a large fraction of the human population. Retrospective studies can be used to map recent movements of infected people, pinpointing the mosquito subpopulation from which they acquired the infection and others to which they may have transmitted it.
Conflict of interest statement
Figures
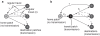






References
-
- Pearn J. Arthropods and disease: the evolution of knowledge about vector-borne disease. 2004. The International Society of the History of Medicine, 39th International Congress Bari, Italy.
-
- McKenzie FE. Why model malaria? Parasitol Today. 2000;16:511–516. - PubMed
-
- Morrison AC, Getis A, Santiago M, Rigau-Perez JG, Reiter P. Exploratory space-time analysis of reported dengue cases during an outbreak in Florida, Puerto Rico, 1991–1992. Am J Trop Med Hyg. 1998;58:287–298. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Molecular Biology Databases

