Generating coherent patterns of activity from chaotic neural networks
- PMID: 19709635
- PMCID: PMC2756108
- DOI: 10.1016/j.neuron.2009.07.018
Generating coherent patterns of activity from chaotic neural networks
Abstract
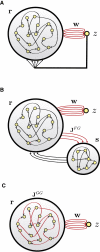
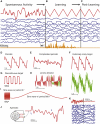
Neural circuits display complex activity patterns both spontaneously and when responding to a stimulus or generating a motor output. How are these two forms of activity related? We develop a procedure called FORCE learning for modifying synaptic strengths either external to or within a model neural network to change chaotic spontaneous activity into a wide variety of desired activity patterns. FORCE learning works even though the networks we train are spontaneously chaotic and we leave feedback loops intact and unclamped during learning. Using this approach, we construct networks that produce a wide variety of complex output patterns, input-output transformations that require memory, multiple outputs that can be switched by control inputs, and motor patterns matching human motion capture data. Our results reproduce data on premovement activity in motor and premotor cortex, and suggest that synaptic plasticity may be a more rapid and powerful modulator of network activity than generally appreciated.
Figures


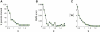



Comment in
-
Harnessing chaos in recurrent neural networks.Neuron. 2009 Aug 27;63(4):423-5. doi: 10.1016/j.neuron.2009.08.003. Neuron. 2009. PMID: 19709625 Free PMC article. Review.
References
-
- Abarbanel HD, Creveling DR, Jeanne JM. Estimation of parameters in nonlinear systems using balanced synchronization. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 2008;77:016208. - PubMed
-
- Atiya AF, Parlos AG. New results on recurrent network training: Unifying the algorithms and accelerating convergence. IEEE Transactions on Neural Networks. 2000;11:697–709. - PubMed
-
- Amit DJ, Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb. Cortex. 1997;7:237–252. - PubMed
-
- Bertchinger N, Natschläger T. Real-time computation at the edge of chaos in recurrent neural networks. Neural Comput. 2004;16:1413–1436. - PubMed
-
- Brunel N. Dynamics of networks of randomly connected excitatory and inhibitory spiking neurons. J. Physiol. Paris. 2000;94:445–463. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

