Feasible stability region in the frontal plane during human gait

Abstract

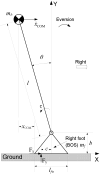
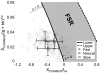
The inability to adequately control the motion of the center of mass (COM) in the frontal plane may result in a loss of balance causing a sideways fall during human gait. The primary purposes of this study were (1) to derive the feasible stability region (FSR) in the mediolateral direction, and (2) to compare the FSR with the COM motion state taken from 193 trials among 39 young subjects at liftoff during walking at different speeds. The lower boundary of the FSR was derived, at a given initial COM location, as the minimum rightward COM velocity, at liftoff of the left foot, required to bring the COM into the base of support (BOS), i.e., the right (stance) foot, as the COM velocity diminishes. The upper boundary was derived as the maximum rightward COM velocity, beyond which the left foot must land to the right of the right foot (BOS) in order to prevent a fall. We established a 2-link human model and employed dynamic optimization to estimate these threshold values for velocity. For a range of initial COM positions, simulated annealing algorithm was used to search for the threshold velocity values. Our study quantified the extent to which mediolateral balance can still be maintained without resorting to a crossover step (the left foot lands to the right of the BOS) for balance recovery. The derived FSR is in good agreement with our gait experimental results.

Fig. 1

Schematic of the 2-link (the right foot and the rest of the body), frontal-plane model of the human body. The right foot is the base of support (BOS) of the model. The ankle joint is modeled as a 1-degree-of-freedom hinge joint, and its angle θ represents the generalized coordinates of the model. The foot and body anthropometric parameters were determined based on a typical male with body height at 1.78m and body mass at 80kg. The positive X-axis is to the right, and the positive Y-axis is upward. Positive joint rotation is along the positive Z-axis (counterclockwise).

Fig. 2

(a) The schematic for approximating the base of support (BOS, the sole) which is the right foot in this study. The BOS is represented by a decagon. Ten vertexes of the decagon, as indicated by the open circles, are the toe end (1), the heel (2), the first metatarsal joint (3), the fifth metatarsal joint (4), two ends of the heel width (5 and 6); vertexes of 7 and 8 are between 1 and 3, and between 1 and 4, respectively; vertexes of 9 and 10 are between 2 and 5, and between 2 and 6, respectively. The definitions of foot length, foot widths, and ball length were adopted from the literature. The reference point for calculating the relative position of the center of mass (COM) to the BOS is the most leftward point on the outline of the BOS. In all simulations, the reference point was the position of the first metatarsal joint because we assume that the foot is along the Z axis. When applying this BOS definition to experimental data, the reference point might be altered due to foot's orientation deviating from the Z asix, as shown in (b).

Fig. 3

The flow chart of the simulation and optimization utilized in the present study to derive the feasible stability region boundaries. Simulated annealing algorithm (SAA) was adopted to conduct the optimization portion. The iteration was terminated when the improvement in the cost function was less than 10^-3 for 500 consecutive function evaluations. Also shown are the values of the weights employed in the cost function.

Fig. 4

A representative simulation result of the center of mass (COM) motion state trajectory for the lower boundary of the feasible stability region (FSR) in the frontal plane (a), horizontal acceleration of the COM and time history of ankle joint moment with positive as the inversion moment (b), ankle angle and angular velocity (c), and ground reaction force (d) of a successful lateral balance recovery with an initial COM position of -0.75 (normalized to foot width, l_fw). In (a), the open diamond marks the starting point of the COM motion state for this simulation sample. Also shown is the FSR (gray area) with the lower boundary (thick solid line) and the upper boundary (thick dashed line) to control the body balance. The COM position is relative to the BOS and normalized to foot width (l_fw). The velocity of the COM was normalized to $\sqrt{g\times bh}$, where g is the gravitational acceleration, and bh is body height. In (d), the ground reaction forces are normalized to body weight (bw).

Fig. 5

The feasible stability region (FSR) to control balance in the frontal plane and the initial COM motion state in the mediolateral (ML) direction during gait experiments. The COM motion state in the ML direction at the instant of left liftoff were from 193 trials among 39 young subjects walking at fast (n = 61), natural (n = 69), and slow (n = 63) speeds. Also shown are the corresponding mean ± SD values of the COM motion state for these subjects. The thin dashed lines indicate the ML stability, s, for given COM motion states. The stability magnitude (s) is defined as the shortest distance from the given COM motion state to the boundary.