Probabilistic combination of slant information: weighted averaging and robustness as optimal percepts
- PMID: 19761341
- PMCID: PMC2940417
- DOI: 10.1167/9.9.8
Probabilistic combination of slant information: weighted averaging and robustness as optimal percepts
Abstract
Depth perception involves combining multiple, possibly conflicting, sensory measurements to estimate the 3D structure of the viewed scene. Previous work has shown that the perceptual system combines measurements using a statistically optimal weighted average. However, the system should only combine measurements when they come from the same source. We asked whether the brain avoids combining measurements when they differ from one another: that is, whether the system is robust to outliers. To do this, we investigated how two slant cues-binocular disparity and texture gradients-influence perceived slant as a function of the size of the conflict between the cues. When the conflict was small, we observed weighted averaging. When the conflict was large, we observed robust behavior: perceived slant was dictated solely by one cue, the other being rejected. Interestingly, the rejected cue was either disparity or texture, and was not necessarily the more variable cue. We modeled the data in a probabilistic framework, and showed that weighted averaging and robustness are predicted if the underlying likelihoods have heavier tails than Gaussians. We also asked whether observers had conscious access to the single-cue estimates when they exhibited robustness and found they did not, i.e. they completely fused despite the robust percepts.
Figures



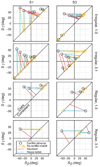




Similar articles
-
Slant from texture and disparity cues: optimal cue combination.J Vis. 2004 Dec 1;4(12):967-92. doi: 10.1167/4.12.1. J Vis. 2004. PMID: 15669906
-
Perceptual biases and cue weighting in perception of 3D slant from texture and stereo information.J Vis. 2015 Feb 10;15(2):14. doi: 10.1167/15.2.14. J Vis. 2015. PMID: 25761332
-
Focus cues affect perceived depth.J Vis. 2005 Dec 15;5(10):834-62. doi: 10.1167/5.10.7. J Vis. 2005. PMID: 16441189 Free PMC article.
-
Bayesian modeling of cue interaction: bistability in stereoscopic slant perception.J Opt Soc Am A Opt Image Sci Vis. 2003 Jul;20(7):1398-406. doi: 10.1364/josaa.20.001398. J Opt Soc Am A Opt Image Sci Vis. 2003. PMID: 12868644
-
The Human Brain in Depth: How We See in 3D.Annu Rev Vis Sci. 2016 Oct 14;2:345-376. doi: 10.1146/annurev-vision-111815-114605. Epub 2016 Jul 22. Annu Rev Vis Sci. 2016. PMID: 28532360 Review.
Cited by
-
Stereoscopy and the Human Visual System.SMPTE Motion Imaging J. 2012 May;121(4):24-43. doi: 10.5594/j18173. SMPTE Motion Imaging J. 2012. PMID: 23144596 Free PMC article.
-
Efficient coding and statistically optimal weighting of covariance among acoustic attributes in novel sounds.PLoS One. 2012;7(1):e30845. doi: 10.1371/journal.pone.0030845. Epub 2012 Jan 23. PLoS One. 2012. PMID: 22292057 Free PMC article. Clinical Trial.
-
Enhancement of visual cues to self-motion during a visual/vestibular conflict.PLoS One. 2023 Mar 15;18(3):e0282975. doi: 10.1371/journal.pone.0282975. eCollection 2023. PLoS One. 2023. PMID: 36920954 Free PMC article.
-
Stereo slant discrimination of planar 3D surfaces: Frontoparallel versus planar matching.J Vis. 2022 Apr 6;22(5):6. doi: 10.1167/jov.22.5.6. J Vis. 2022. PMID: 35467704 Free PMC article.
-
Risk-sensitivity in Bayesian sensorimotor integration.PLoS Comput Biol. 2012;8(9):e1002698. doi: 10.1371/journal.pcbi.1002698. Epub 2012 Sep 27. PLoS Comput Biol. 2012. PMID: 23028294 Free PMC article.
References
-
- Alais D, Burr D. The ventriloquist effect results from near-optimal bimodal integration. Current Biology. 2004;14:257–262. - PubMed
-
- Arnold RD, Binford TO. Geometric constraints in stereo vision. SPIE: Image Processing for Missile Guidance. 1980;238:281–292.
-
- Backus BT, Banks MS, van Ee R, Crowell JA. Horizontal and vertical disparity, eye position, and stereoscopic slant perception. Vision Research. 1999;39:1143–1170. - PubMed
-
- Banks MS, Backus BT. Extra-retinal and perspective cues cause the small range of the induced effect. Vision Research. 1998;38:187–194. - PubMed
-
- Box GEP, Tiao GC. Bayesian inference in statistical analysis. New York: John Wiley & Sons; 1992. Wiley Classics Library edition.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

