Mechanism of amido-thiourea catalyzed enantioselective imine hydrocyanation: transition state stabilization via multiple non-covalent interactions
- PMID: 19778044
- PMCID: PMC2783581
- DOI: 10.1021/ja9058958
Mechanism of amido-thiourea catalyzed enantioselective imine hydrocyanation: transition state stabilization via multiple non-covalent interactions
Abstract
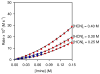
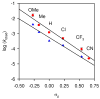
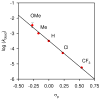
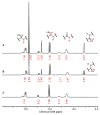
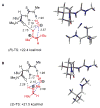
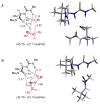
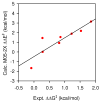
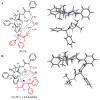
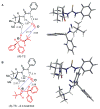
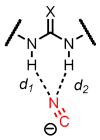
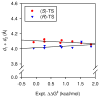
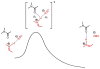
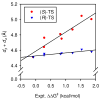
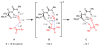
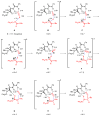
An experimental and computational investigation of amido-thiourea promoted imine hydrocyanation has revealed a new and unexpected mechanism of catalysis. Rather than direct activation of the imine by the thiourea, as had been proposed previously in related systems, the data are consistent with a mechanism involving catalyst-promoted proton transfer from hydrogen isocyanide to imine to generate diastereomeric iminium/cyanide ion pairs that are bound to catalyst through multiple noncovalent interactions; these ion pairs collapse to form the enantiomeric alpha-aminonitrile products. This mechanistic proposal is supported by the observation of a statistically significant correlation between experimental and calculated enantioselectivities induced by eight different catalysts (P << 0.01). The computed models reveal a basis for enantioselectivity that involves multiple stabilizing and destabilizing interactions between substrate and catalyst, including thiourea-cyanide and amide-iminium interactions.
Figures
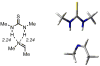

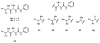


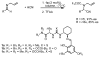
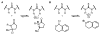
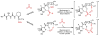

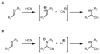
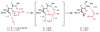

References
-
-
Review, historical perspective, and leading references: Doyle AG, Jacobsen EN. Chem Rev. 2007;107:5713–5743.
-
-
-
For classic examples, see: Johnson JS, Evans DA. Acc Chem Res. 2000;33:325–335.
-
-
- Trost BM, Machacek MR, Aponick A. Acc Chem Res. 2006;39:747–760. - PubMed
-
-
Recent reviews: Lelais G, MacMillan DWC. Aldrichimica Acta. 2006;39:79–87.Mukherjee S, Yang JW, Hoffmann S, List B. Chem Rev. 2007;107:5471–5569.
-
-
-
For a detailed discussion, see: Israelachvili J. Intermolecular & Surface Forces. 2. Academic Press; London: 1991. pp. 109–121.The strength of repulsive non-bonding interactions is roughly proportional to (1/r)12. Within this model, a 25% increase in r leads to a 93% decrease in interaction energy
-
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

