Resolving the impact of waiting time distributions on the persistence of measles
- PMID: 19793743
- PMCID: PMC2842776
- DOI: 10.1098/rsif.2009.0284
Resolving the impact of waiting time distributions on the persistence of measles
Abstract
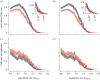
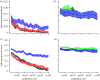
Measles epidemics in human populations exhibit what is perhaps the best empirically characterized, and certainly the most studied, stochastic persistence threshold in population biology. A critical community size (CCS) of around 250,000-500,000 separates populations where measles is predominantly persistent from smaller communities where there are frequent extinctions of measles between major epidemics. The fundamental mechanisms contributing to this pattern of persistence, which are long-lasting immunity to re-infection, recruitment of susceptibles, seasonality in transmission, age dependence of transmission and the spatial coupling between communities, have all been quantified and, to a greater or lesser level of success, captured by theoretical models. Despite these successes there has not been a consensus over whether simple models can successfully predict the value of the CCS, or indeed which mechanisms determine the persistence of measles over a broader range of population sizes. Specifically, the level of the CCS has been thought to be particularly sensitive to the detailed stochastic dynamics generated by the waiting time distribution (WTD) in the infectious and latent periods. We show that the relative patterns of persistence between models with different WTDs are highly sensitive to the criterion of comparison-in particular, the statistical measure of persistence that is employed. To this end, we introduce two new statistical measures of persistence-fade-outs post epidemic and fade-outs post invasion. Contrary to previous reports, we demonstrate that, no matter the choice of persistence measure, appropriately parametrized models of measles demonstrate similar predictions for the level of the CCS.
Figures




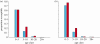
Similar articles
-
Seasonality and the persistence and invasion of measles.Proc Biol Sci. 2007 May 7;274(1614):1133-41. doi: 10.1098/rspb.2006.0030. Proc Biol Sci. 2007. PMID: 17327206 Free PMC article.
-
Probabilistic measures of persistence and extinction in measles (meta)populations.Ecol Lett. 2013 Aug;16(8):985-94. doi: 10.1111/ele.12124. Epub 2013 Jun 20. Ecol Lett. 2013. PMID: 23782847 Free PMC article.
-
Understanding the persistence of measles: reconciling theory, simulation and observation.Proc Biol Sci. 2002 Feb 22;269(1489):335-43. doi: 10.1098/rspb.2001.1898. Proc Biol Sci. 2002. PMID: 11886620 Free PMC article.
-
Spatial heterogeneity, nonlinear dynamics and chaos in infectious diseases.Stat Methods Med Res. 1995 Jun;4(2):160-83. doi: 10.1177/096228029500400205. Stat Methods Med Res. 1995. PMID: 7582203 Review.
-
Epidemiology of communicable disease in small populations.J Mol Med (Berl). 1998 Feb;76(2):111-6. doi: 10.1007/s001090050198. J Mol Med (Berl). 1998. PMID: 9500676 Review.
Cited by
-
Eight challenges in modelling disease ecology in multi-host, multi-agent systems.Epidemics. 2015 Mar;10:26-30. doi: 10.1016/j.epidem.2014.10.001. Epub 2014 Dec 9. Epidemics. 2015. PMID: 25843378 Free PMC article.
-
Assessing the potential impact of transmission during prolonged viral shedding on the effect of lockdown relaxation on COVID-19.PLoS Comput Biol. 2021 Jan 29;17(1):e1008609. doi: 10.1371/journal.pcbi.1008609. eCollection 2021 Jan. PLoS Comput Biol. 2021. PMID: 33513139 Free PMC article.
-
Evidence of cryptic incidence in childhood diseases.Proc Biol Sci. 2017 Aug 30;284(1861):20171268. doi: 10.1098/rspb.2017.1268. Proc Biol Sci. 2017. PMID: 28855364 Free PMC article.
-
Natural immune boosting in pertussis dynamics and the potential for long-term vaccine failure.Proc Natl Acad Sci U S A. 2011 Apr 26;108(17):7259-64. doi: 10.1073/pnas.1014394108. Epub 2011 Mar 21. Proc Natl Acad Sci U S A. 2011. PMID: 21422281 Free PMC article.
-
Direct and indirect effects of rotavirus vaccination: comparing predictions from transmission dynamic models.PLoS One. 2012;7(8):e42320. doi: 10.1371/journal.pone.0042320. Epub 2012 Aug 13. PLoS One. 2012. PMID: 22912699 Free PMC article.
References
-
- Anderson D., Watson R. 1980. On the spread of a disease with gamma distributed latent and infectious periods. Biometrika 67, 191–198. (10.1093/biomet/67.1.191) - DOI
-
- Anderson R. M., May R. M. 1991. Infectious diseases of humans: dynamics and control. New York, NY: Oxford University Press.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

