Spherical topology in cardiac simulations
- PMID: 19794820
- PMCID: PMC2707797
- DOI: 10.2976/1.3074105
Spherical topology in cardiac simulations
Abstract
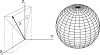
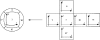
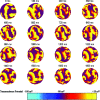
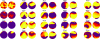
Computational simulations of the electrodynamics of cardiac fibrillation yield a great deal of useful data and provide a framework for theoretical explanations of heart behavior. Extending the application of these mathematical models to defibrillation studies requires that a simulation should sustain fibrillation without defibrillation intervention. In accordance with the critical mass hypothesis, the simulated tissue should be of a large enough size. The choice of biperiodic boundary conditions sustains fibrillation for a longer duration than no-flux boundary conditions for a given area, and so is commonly invoked. Here, we show how this leads to a boundary condition artifact that may complicate the analysis of defibrillation efficacy; we implement an alternative coordinate scheme that utilizes spherical shell topology and mitigates singularities in the Laplacian found with the usual spherical curvilinear coordinate system.
Figures

Similar articles
-
[Mechanisms of electrical defibrillation].Herzschrittmacherther Elektrophysiol. 1997 Mar;8(1):4-14. doi: 10.1007/BF03042473. Herzschrittmacherther Elektrophysiol. 1997. PMID: 19495673 German.
-
The topology of defibrillation.J Theor Biol. 2004 Oct 21;230(4):459-73. doi: 10.1016/j.jtbi.2003.11.033. J Theor Biol. 2004. PMID: 15363669
-
Program Code Generator for Cardiac Electrophysiology Simulation with Automatic PDE Boundary Condition Handling.PLoS One. 2015 Sep 10;10(9):e0136821. doi: 10.1371/journal.pone.0136821. eCollection 2015. PLoS One. 2015. PMID: 26356082 Free PMC article.
-
Imaging of Ventricular Fibrillation and Defibrillation: The Virtual Electrode Hypothesis.Adv Exp Med Biol. 2015;859:343-65. doi: 10.1007/978-3-319-17641-3_14. Adv Exp Med Biol. 2015. PMID: 26238060 Free PMC article. Review.
-
Progressive depolarization: a unified hypothesis for defibrillation and fibrillation induction by shocks.J Cardiovasc Electrophysiol. 1998 May;9(5):529-52. doi: 10.1111/j.1540-8167.1998.tb01847.x. J Cardiovasc Electrophysiol. 1998. PMID: 9607463 Review.
References
-
- Calhoun, D A, Helzel, C, and LeVeque, R J (2008). “Logically rectangular grids and finite volume methods for PDEs in circular and spherical domains.” SIAM Rev. SIREAD10.1137/060664094 50, 723–752. - DOI
-
- Cromwell, P R (1997). Polyhedra: “One of the Most Charming Chapters of Geometry,” Cambridge University Press, Cambridge, UK.
-
- Eriksson, K, Estep, D, Hansbro, P, and Johnson, C (1996). Computational Differential Equations, Studentlitteratur, Sweden.
LinkOut - more resources
Full Text Sources
