Spherical topology in cardiac simulations

Abstract

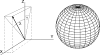
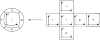
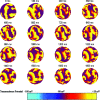
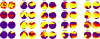
Computational simulations of the electrodynamics of cardiac fibrillation yield a great deal of useful data and provide a framework for theoretical explanations of heart behavior. Extending the application of these mathematical models to defibrillation studies requires that a simulation should sustain fibrillation without defibrillation intervention. In accordance with the critical mass hypothesis, the simulated tissue should be of a large enough size. The choice of biperiodic boundary conditions sustains fibrillation for a longer duration than no-flux boundary conditions for a given area, and so is commonly invoked. Here, we show how this leads to a boundary condition artifact that may complicate the analysis of defibrillation efficacy; we implement an alternative coordinate scheme that utilizes spherical shell topology and mitigates singularities in the Laplacian found with the usual spherical curvilinear coordinate system.

Figure 1. Alternative coordinate system (χ

,γ) used to solve the Laplacian on the surface of a sphere. The point P lies on the sphere of radius R and is indicated by the position vector. The position vector of P projected into the xz-plane lies at an angle χ off the z-axis, and the position vector of P projected into the yz-plane lies at an angle γ off the z-axis.

Figure 2. Mapping of the six faces onto the surface of the sphere.

The “cross” figure on the right is folded into a cube, and the cube is inflated to produce the sphere on the left. This figure is a modified version of Fig. 3 in J. Comput. Phy.124, 93–114 by Ronchi et al. (1996).

Figure 3. Fibrillation on the spherical coordinate system.

Shown is one side of the sphere with a 120 ms frame rate. A randomly initialized distribution of rotary waves (shown at 0 ms) evolves into the distribution eventually shown in the 1800 ms frame. The rear view of the sphere looks qualitatively similar to this front view and is not shown. The color bar shows the relation between color and transmembrane potential.

Figure 4. The development of poles of opposite chirality.

Both hemispheres of the sphere are shown for each time. The simulation is initialized in the 0 ms frame and quickly progresses to a relatively simple state of VF (few phase singularities) shown in the 48 ms frame. In frame 216 ms it is evident that poles of opposite chirality develop. While the singularities are not “pinned” to a particular location on the tissue, the poles where the phase singularities meander are a small area—analogous to precession but with no period of precession noted. We see this development of poles of opposite chirality in many of our simulations that are properly initialized to sustain fibrillation. The color map is the same as Fig. 3.

Figure 5. Simulation showing how external electrical stimulation is accurately reproduced in this coordinate system.

One face of the sphere is observed for 350 ms. Observe the stimuli pointed out at 192 and 288 ms. Regional capture is achieved, leading to global entrainment (see 350 ms). The protocol calls for pacing for 3 s, therefore a diastolic state is eventually achieved when the pacing ceases. The color map is the same as Fig. 3.