Phylodynamics of infectious disease epidemics

Abstract

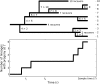
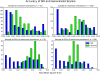
We present a formalism for unifying the inference of population size from genetic sequences and mathematical models of infectious disease in populations. Virus phylogenies have been used in many recent studies to infer properties of epidemics. These approaches rely on coalescent models that may not be appropriate for infectious diseases. We account for phylogenetic patterns of viruses in susceptible-infected (SI), susceptible-infected-susceptible (SIS), and susceptible-infected-recovered (SIR) models of infectious disease, and our approach may be a viable alternative to demographic models used to reconstruct epidemic dynamics. The method allows epidemiological parameters, such as the reproductive number, to be estimated directly from viral sequence data. We also describe patterns of phylogenetic clustering that are often construed as arising from a short chain of transmissions. Our model reproduces the moments of the distribution of phylogenetic cluster sizes and may therefore serve as a null hypothesis for cluster sizes under simple epidemiological models. We examine a small cross-sectional sample of human immunodeficiency (HIV)-1 sequences collected in the United States and compare our results to standard estimates of effective population size. Estimated prevalence is consistent with estimates of effective population size and the known history of the HIV epidemic. While our model accurately estimates prevalence during exponential growth, we find that periods of decline are harder to identify.

Figure 1.—

An example of a phylogeny that could be generated by an epidemic process. The number of lineages at time t for a population observed at time T is plotted below. A branch in the tree corresponds to a transmission event, and as a lineage is traced backward in time, it traverses multiple infected hosts.

Figure 2.—

The moments of the cluster size distribution over time as calculated by Equations 3 and 9 (lines, log scale). Four trajectories of the cluster size moments were generated for 4 sample times T. And for each trajectory, simulated moments were calculated for 10 threshold times t. Error bars show the 90% interval for 100 agent-based simulations [N = 10⁵ and I(0) = 1%]. The SIR model is . Epidemic prevalence (dotted line) is shown on the right axis. Transmission rate β = 1, and recovery rate μ = 0.3.

Figure 3.—

Root mean square error of SIR and generalized skyline estimates of epidemic prevalence. Data are based on 300 simulated epidemics (R₀ = 2). RMSE is averaged over 100 time points.

Figure 4.—

The empirical distribution of coalescence times based on 150 simulated SIR epidemics. Transmission rate = 2, recovery rate = 1. The expected distribution based on Equation 11 is shown in red.

Figure 5.—

Left: Estimated epidemic prevalence (logarithmic scale) of HIV among MSM in the United States. A solution to Equation 16 is compared to the skyline plot, rescaled such that minimum effective population size equals minimum prevalence. The thin lines show 95% confidence intervals. Right: Estimated cumulative incidence of HIV among MSM vs. time (years prior to 1993). A solution to Equation 16 is compared to estimates based on sero-surveillance data (Hall et al. 2008).

Figure 6.—

The mean cluster size (dashes) and variance of cluster sizes (dotted line) are calculated from the empirical observations from the ACTG241 sequences (dashed lines) and compared to our best-fit SIR model (solid lines). The horizontal axis gives the clustering threshold as the year of the MRCA of a cluster.