Combining fungal biopesticides and insecticide-treated bednets to enhance malaria control
- PMID: 19798436
- PMCID: PMC2742557
- DOI: 10.1371/journal.pcbi.1000525
Combining fungal biopesticides and insecticide-treated bednets to enhance malaria control
Abstract
In developing strategies to control malaria vectors, there is increased interest in biological methods that do not cause instant vector mortality, but have sublethal and lethal effects at different ages and stages in the mosquito life cycle. These techniques, particularly if integrated with other vector control interventions, may produce substantial reductions in malaria transmission due to the total effect of alterations to multiple life history parameters at relevant points in the life-cycle and transmission-cycle of the vector. To quantify this effect, an analytically tractable gonotrophic cycle model of mosquito-malaria interactions is developed that unites existing continuous and discrete feeding cycle approaches. As a case study, the combined use of fungal biopesticides and insecticide treated bednets (ITNs) is considered. Low values of the equilibrium EIR and human prevalence were obtained when fungal biopesticides and ITNs were combined, even for scenarios where each intervention acting alone had relatively little impact. The effect of the combined interventions on the equilibrium EIR was at least as strong as the multiplicative effect of both interventions. For scenarios representing difficult conditions for malaria control, due to high transmission intensity and widespread insecticide resistance, the effect of the combined interventions on the equilibrium EIR was greater than the multiplicative effect, as a result of synergistic interactions between the interventions. Fungal biopesticide application was found to be most effective when ITN coverage was high, producing significant reductions in equilibrium prevalence for low levels of biopesticide coverage. By incorporating biological mechanisms relevant to vectorial capacity, continuous-time vector population models can increase their applicability to integrated vector management.
Conflict of interest statement
The author has declared that no competing interests exist.
Figures

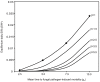
 ) for different values of the shape parameter
) for different values of the shape parameter  and other parameters as in Table 1. For
and other parameters as in Table 1. For  values of the equilibrium daily EIR obtained by analytic derivation (open diamonds) and simulation (black squares) are compared. Sublethal effects of fungal infection on mosquito feeding biology are not incorporated (
values of the equilibrium daily EIR obtained by analytic derivation (open diamonds) and simulation (black squares) are compared. Sublethal effects of fungal infection on mosquito feeding biology are not incorporated ( &
&  ).
).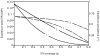
 ). Lines labelled 1 correspond to the ITN intervention parameters in Table 1, and lines labelled 2 correspond to the case where the ITN intervention has no effect on mosquito mortality (other ITN intervention parameters are as in Table 1).
). Lines labelled 1 correspond to the ITN intervention parameters in Table 1, and lines labelled 2 correspond to the case where the ITN intervention has no effect on mosquito mortality (other ITN intervention parameters are as in Table 1).
 ) for three values of the daily probability of fungal infection (
) for three values of the daily probability of fungal infection ( ): A, C = 0.1 B, C = 0.5 C, C = 0.9. Lines represent varying sublethal effects of fungal infection on mosquito feeding biology, including no sublethal effects (solid lines), a 25% decrease in the daily probability of finding a blood meal (
): A, C = 0.1 B, C = 0.5 C, C = 0.9. Lines represent varying sublethal effects of fungal infection on mosquito feeding biology, including no sublethal effects (solid lines), a 25% decrease in the daily probability of finding a blood meal ( ) and a 25% increase in the duration of the non-host-seeking stage (
) and a 25% increase in the duration of the non-host-seeking stage ( ) in fungal pathogen-infected mosquitoes (dashed lines), a 50% decrease in
) in fungal pathogen-infected mosquitoes (dashed lines), a 50% decrease in  and a 50% increase in
and a 50% increase in  (dotted lines), and a 75% decrease in
(dotted lines), and a 75% decrease in  and a 75% increase in
and a 75% increase in  (dot-dashed lines). Other parameters are given in Table 1.
(dot-dashed lines). Other parameters are given in Table 1.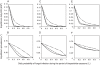
 ): A–B.
): A–B.  , C–D.
, C–D.  , E–F.
, E–F.  . Lines represent biopesticide exposure periods (see text) corresponding to
. Lines represent biopesticide exposure periods (see text) corresponding to  (solid lines),
(solid lines),  (dashed lines) and
(dashed lines) and  (dot-dashed lines).
(dot-dashed lines).
 ) for varying ITN coverage (
) for varying ITN coverage ( ) and daily probability of fungal infection during the period of biopesticide exposure (CE), for different ITN intervention parameters: A. The ITN intervention parameters given in Table 1, B. The ITN intervention does not affect mosquito mortality (other ITN intervention parameters are as in Table 1). The mean time to death from fungal infection is
) and daily probability of fungal infection during the period of biopesticide exposure (CE), for different ITN intervention parameters: A. The ITN intervention parameters given in Table 1, B. The ITN intervention does not affect mosquito mortality (other ITN intervention parameters are as in Table 1). The mean time to death from fungal infection is  .
.
 ) as a function of the ITN coverage (
) as a function of the ITN coverage ( ). Points represent different ITN intervention parameters, including the parameters given in Table 1 (open circles) and the case where the ITN intervention does not affect mosquito mortality (crosses). All combinations of mean times to death from fungal infection (
). Points represent different ITN intervention parameters, including the parameters given in Table 1 (open circles) and the case where the ITN intervention does not affect mosquito mortality (crosses). All combinations of mean times to death from fungal infection ( ) of
) of  , and values of the daily probability of fungal infection during the period of biopesticide exposure (CE) of CE = 0.2, 0.4, 0.6 and 0.8, are shown. Panels show different levels of transmission intensity: A. Annual EIR = 47.8, B. Annual EIR = 412.
, and values of the daily probability of fungal infection during the period of biopesticide exposure (CE) of CE = 0.2, 0.4, 0.6 and 0.8, are shown. Panels show different levels of transmission intensity: A. Annual EIR = 47.8, B. Annual EIR = 412.
 ) for varying ITN coverage (
) for varying ITN coverage ( ) and daily probability of fungal infection during the period of biopesticide exposure (CE), for different ITN intervention parameters: A. The ITN intervention parameters given in Table 1, B. The ITN intervention does not affect mosquito mortality (other ITN intervention parameters are as in Table 1). The transmission intensity is high (annual EIR = 412). The mean time to death from fungal infection is
) and daily probability of fungal infection during the period of biopesticide exposure (CE), for different ITN intervention parameters: A. The ITN intervention parameters given in Table 1, B. The ITN intervention does not affect mosquito mortality (other ITN intervention parameters are as in Table 1). The transmission intensity is high (annual EIR = 412). The mean time to death from fungal infection is  .
.
 ) for varying ITN coverage (
) for varying ITN coverage ( ) and daily probability of fungal infection during the period of biopesticide exposure (CE). The transmission intensity is low (annual EIR = 1.5). The mean time to death from fungal infection is
) and daily probability of fungal infection during the period of biopesticide exposure (CE). The transmission intensity is low (annual EIR = 1.5). The mean time to death from fungal infection is  .
.Similar articles
-
Integrated vector management for malaria control.Malar J. 2008 Dec 11;7 Suppl 1(Suppl 1):S4. doi: 10.1186/1475-2875-7-S1-S4. Malar J. 2008. PMID: 19091038 Free PMC article. Review.
-
An elaborated feeding cycle model for reductions in vectorial capacity of night-biting mosquitoes by insecticide-treated nets.Malar J. 2007 Jan 25;6:10. doi: 10.1186/1475-2875-6-10. Malar J. 2007. PMID: 17254339 Free PMC article.
-
Lethal and pre-lethal effects of a fungal biopesticide contribute to substantial and rapid control of malaria vectors.PLoS One. 2011;6(8):e23591. doi: 10.1371/journal.pone.0023591. Epub 2011 Aug 29. PLoS One. 2011. PMID: 21897846 Free PMC article.
-
Malaria vector control: current and future strategies.Trends Parasitol. 2009 Mar;25(3):101-4. doi: 10.1016/j.pt.2008.12.002. Epub 2009 Jan 23. Trends Parasitol. 2009. PMID: 19168392
-
Malaria vector control: from past to future.Parasitol Res. 2011 Apr;108(4):757-79. doi: 10.1007/s00436-010-2232-0. Epub 2011 Jan 13. Parasitol Res. 2011. PMID: 21229263 Review.
Cited by
-
Exploiting the behaviour of wild malaria vectors to achieve high infection with fungal biocontrol agents.Malar J. 2012 Mar 26;11:87. doi: 10.1186/1475-2875-11-87. Malar J. 2012. PMID: 22449130 Free PMC article.
-
Malaria elimination on Hainan Island despite climate change.Commun Med (Lond). 2022 Feb 9;2:12. doi: 10.1038/s43856-022-00073-z. eCollection 2022. Commun Med (Lond). 2022. PMID: 35603266 Free PMC article.
-
Studies on Fungal Cultural Filtrates against Adult Culex quinquefasciatus (Diptera: Culicidae) a Vector of Filariasis.J Parasitol Res. 2011;2011:147373. doi: 10.1155/2011/147373. Epub 2011 Oct 29. J Parasitol Res. 2011. PMID: 22132305 Free PMC article.
-
Prospective malaria control using entomopathogenic fungi: comparative evaluation of impact on transmission and selection for resistance.Malar J. 2012 Nov 22;11:383. doi: 10.1186/1475-2875-11-383. Malar J. 2012. PMID: 23171286 Free PMC article.
-
Transgenic Metarhizium pingshaense synergistically ameliorates pyrethroid-resistance in wild-caught, malaria-vector mosquitoes.PLoS One. 2018 Sep 7;13(9):e0203529. doi: 10.1371/journal.pone.0203529. eCollection 2018. PLoS One. 2018. PMID: 30192847 Free PMC article.
References
-
- Stratton L, O'Neill MS, Kruk ME, Bell ML. The persistent problem of malaria: Addressing the fundamental causes of a global killer. Soc Sci Med. 2008;67:854–862. - PubMed
-
- Haworth J. The global distribution of malaria and the present control efforts. In: Wernsdorfer MM,I,, editor. Malaria. Edinburgh, United Kingdom: Churchill Livingstone; 1988. pp. 1379–1420.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Medical
Research Materials

