A new methodology for the estimation of fiber populations in the white matter of the brain with the Funk-Radon transform
- PMID: 19815078
- PMCID: PMC4026251
- DOI: 10.1016/j.neuroimage.2009.09.070
A new methodology for the estimation of fiber populations in the white matter of the brain with the Funk-Radon transform
Abstract
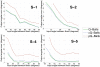
The Funk-Radon Transform (FRT) is a powerful tool for the estimation of fiber populations with High Angular Resolution Diffusion Imaging (HARDI). It is used in Q-Ball imaging (QBI), and other HARDI techniques such as the recent Orientation Probability Density Transform (OPDT), to estimate fiber populations with very few restrictions on the diffusion model. The FRT consists in the integration of the attenuation signal, sampled by the MRI scanner on the unit sphere, along equators orthogonal to the directions of interest. It is easily proved that this calculation is equivalent to the integration of the diffusion propagator along such directions, although a characteristic blurring with a Bessel kernel is introduced. Under a different point of view, the FRT can be seen as an efficient way to compute the angular part of the integral of the attenuation signal in the plane orthogonal to each direction of the diffusion propagator. In this paper, Stoke's theorem is used to prove that the FRT can in fact be used to compute accurate estimates of the true integrals defining the functions of interest in HARDI, keeping the diffusion model as little restrictive as possible. Varying the assumptions on the attenuation signal, we derive new estimators of fiber orientations, generalizing both Q-Balls and the OPDT. Extensive experiments with both synthetic and real data have been intended to show that the new techniques improve existing ones in many situations.
Figures
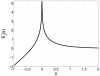
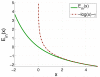
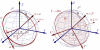
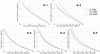
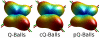

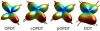



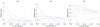
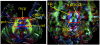


References
-
- Abramowitz M, Stegun IA, editors. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover; New York: 1972.
-
- Aganj I, Lenglet C, Sapiro G. ODF reconstruction in Q–Ball imaging with solid angle consideration; Proceedings of the 6th International Symposium on Biomedical Imaging: from Nano to Macro. IEEE; 2009a; Jul. pp. 1398–1401. available online: Jan. 2009 http://www.tc.umn.edu/~man/index_files/Publications.htm. - PMC - PubMed
-
- Alexander D. Information Processing in Medical Imaging. Glenwood Springs, CO, USA: Jul. 2005. Maximum entropy spherical deconvolution for diffusion MRI; pp. 76–87. - PubMed
-
- Anderson A. Measurement of fiber orientation distributions using High Angular Resolution Diffusion Imaging. Magnetic Resonance in Medicine. 2005;54(5):1194–1206. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

