Fast and consistent estimation of species trees using supermatrix rooted triples
- PMID: 19833741
- PMCID: PMC2877557
- DOI: 10.1093/molbev/msp250
Fast and consistent estimation of species trees using supermatrix rooted triples
Abstract
Concatenated sequence alignments are often used to infer species-level relationships. Previous studies have shown that analysis of concatenated data using maximum likelihood (ML) can produce misleading results when loci have differing gene tree topologies due to incomplete lineage sorting. Here, we develop a polynomial time method that utilizes the modified mincut supertree algorithm to construct an estimated species tree from inferred rooted triples of concatenated alignments. We term this method SuperMatrix Rooted Triple (SMRT) and use the notation SMRT-ML when rooted triples are inferred by ML. We use simulations to investigate the performance of SMRT-ML under Jukes-Cantor and general time-reversible substitution models for four- and five-taxon species trees and also apply the method to an empirical data set of yeast genes. We find that SMRT-ML converges to the correct species tree in many cases in which ML on the full concatenated data set fails to do so. SMRT-ML can be conservative in that its output tree is often partially unresolved for problematic clades. We show analytically that when the species tree is clocklike and mutations occur under the Cavender-Farris-Neyman substitution model, as the number of genes increases, SMRT-ML is increasingly likely to infer the correct species tree even when the most likely gene tree does not match the species tree. SMRT-ML is therefore a computationally efficient and statistically consistent estimator of the species tree when gene trees are distributed according to the multispecies coalescent model.
Figures


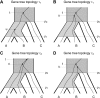
 all alignments of three species, which are then fed through PAUP* to infer a total of
all alignments of three species, which are then fed through PAUP* to infer a total of  rooted triples. These rooted triples are used as input to supertree (Page 2002) to infer a species tree (SMRT-ML). The dashed gray box represents the part of the procedure that is SMRT-ML.
rooted triples. These rooted triples are used as input to supertree (Page 2002) to infer a species tree (SMRT-ML). The dashed gray box represents the part of the procedure that is SMRT-ML.





Similar articles
-
Properties of consensus methods for inferring species trees from gene trees.Syst Biol. 2009 Feb;58(1):35-54. doi: 10.1093/sysbio/syp008. Epub 2009 Jun 4. Syst Biol. 2009. PMID: 20525567 Free PMC article.
-
Species Tree Estimation from Genome-Wide Data with guenomu.Methods Mol Biol. 2017;1525:461-478. doi: 10.1007/978-1-4939-6622-6_18. Methods Mol Biol. 2017. PMID: 27896732
-
Estimating species trees using approximate Bayesian computation.Mol Phylogenet Evol. 2011 May;59(2):354-63. doi: 10.1016/j.ympev.2011.02.019. Epub 2011 Mar 21. Mol Phylogenet Evol. 2011. PMID: 21397706
-
Challenges in Species Tree Estimation Under the Multispecies Coalescent Model.Genetics. 2016 Dec;204(4):1353-1368. doi: 10.1534/genetics.116.190173. Genetics. 2016. PMID: 27927902 Free PMC article. Review.
-
Coalescent methods for estimating phylogenetic trees.Mol Phylogenet Evol. 2009 Oct;53(1):320-8. doi: 10.1016/j.ympev.2009.05.033. Epub 2009 Jun 6. Mol Phylogenet Evol. 2009. PMID: 19501178 Review.
Cited by
-
Comparative genomics of biotechnologically important yeasts.Proc Natl Acad Sci U S A. 2016 Aug 30;113(35):9882-7. doi: 10.1073/pnas.1603941113. Epub 2016 Aug 17. Proc Natl Acad Sci U S A. 2016. PMID: 27535936 Free PMC article.
-
STELAR: a statistically consistent coalescent-based species tree estimation method by maximizing triplet consistency.BMC Genomics. 2020 Feb 10;21(1):136. doi: 10.1186/s12864-020-6519-y. BMC Genomics. 2020. PMID: 32039704 Free PMC article.
-
Quartet inference from SNP data under the coalescent model.Bioinformatics. 2014 Dec 1;30(23):3317-24. doi: 10.1093/bioinformatics/btu530. Epub 2014 Aug 7. Bioinformatics. 2014. PMID: 25104814 Free PMC article.
-
The Meaning and Measure of Concordance Factors in Phylogenomics.Mol Biol Evol. 2024 Nov 1;41(11):msae214. doi: 10.1093/molbev/msae214. Mol Biol Evol. 2024. PMID: 39418118 Free PMC article. Review.
-
CHAPAO: Likelihood and hierarchical reference-based representation of biomolecular sequences and applications to compressing multiple sequence alignments.PLoS One. 2022 Apr 18;17(4):e0265360. doi: 10.1371/journal.pone.0265360. eCollection 2022. PLoS One. 2022. PMID: 35436292 Free PMC article.
References
-
- Aho AV, Sagiv Y, Szymanski TG, Ullman JD. Inferring a tree from lowest common ancestors with an application to the optimization of relational expressions. SIAM J Comput. 1981;10:405–421.
-
- Ané C, Larget B, Baum DA, Smith SD, Rokas A. Bayesian estimation of concordance factors. Mol Biol Evol. 2007;24:412–426. - PubMed
-
- Baum BR. Combining trees as a way of combining data sets for phylogenetic inference, and the desirability of combining gene trees. Taxon. 1992;41:3–10.
-
- Bininda-Emonds ORP. The evolution of supertrees. Trends Ecol Evol. 2004;19:315–322. - PubMed
-
- Bryant D. A classification of consensus methods for phylogenies. In: Janowitz MF, Lapointe F-J, McMorris FR, Mirkin B, Roberts FS, editors. Bioconsensus. Vol. 61. Providence (RI): DIMACS, AMS; 2003. pp. 163–183.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

