Sampling and visualizing creases with scale-space particles
- PMID: 19834216
- PMCID: PMC2891996
- DOI: 10.1109/TVCG.2009.177
Sampling and visualizing creases with scale-space particles
Abstract
Particle systems have gained importance as a methodology for sampling implicit surfaces and segmented objects to improve mesh generation and shape analysis. We propose that particle systems have a significantly more general role in sampling structure from unsegmented data. We describe a particle system that computes samplings of crease features (i.e. ridges and valleys, as lines or surfaces) that effectively represent many anatomical structures in scanned medical data. Because structure naturally exists at a range of sizes relative to the image resolution, computer vision has developed the theory of scale-space, which considers an n-D image as an (n+1)-D stack of images at different blurring levels. Our scale-space particles move through continuous four-dimensional scale-space according to spatial constraints imposed by the crease features, a particle-image energy that draws particles towards scales of maximal feature strength, and an inter-particle energy that controls sampling density in space and scale. To make scale-space practical for large three-dimensional data, we present a spline-based interpolation across scale from a small number of pre-computed blurrings at optimally selected scales. The configuration of the particle system is visualized with tensor glyphs that display information about the local Hessian of the image, and the scale of the particle. We use scale-space particles to sample the complex three-dimensional branching structure of airways in lung CT, and the major white matter structures in brain DTI.
Figures

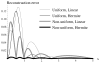
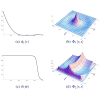


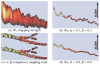
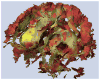

References
-
- Arsigny V, Fillard P, Pennec X, Ayache N. Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magnetic Resonance in Medicine. 2006 August;56(2):411–421. - PubMed
-
- Aylward S, Bullitt E, Pizer S, Eberly D. Intensity ridge and widths for tubular object segmentation and description. Proc. Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA); 1996. pp. 131–138.
-
- Aylward SR, Bullitt E. Initialization, noise, singularities, and scale in height ridge traversal for tubular object centerline extraction. IEEE Trans on Medical Imaging. 2002 Feb;21(2):61–75. - PubMed
-
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractograpy using DT-MRI data. Magnetic Resonance in Medicine. 2000;44:625–632. - PubMed

