Inferring branching pathways in genome-scale metabolic networks

Abstract

Background: A central problem in computational metabolic modelling is how to find biochemically plausible pathways between metabolites in a metabolic network. Two general, complementary frameworks have been utilized to find metabolic pathways: constraint-based modelling and graph-theoretical path finding approaches. In constraint-based modelling, one aims to find pathways where metabolites are balanced in a pseudo steady-state. Constraint-based methods, such as elementary flux mode analysis, have typically a high computational cost stemming from a large number of steady-state pathways in a typical metabolic network. On the other hand, graph-theoretical approaches avoid the computational complexity of constraint-based methods by solving a simpler problem of finding shortest paths. However, while scaling well with network size, graph-theoretic methods generally tend to return more false positive pathways than constraint-based methods.

Results: In this paper, we introduce a computational method, ReTrace, for finding biochemically relevant, branching metabolic pathways in an atom-level representation of metabolic networks. The method finds compact pathways which transfer a high fraction of atoms from source to target metabolites by considering combinations of linear shortest paths. In contrast to current steady-state pathway analysis methods, our method scales up well and is able to operate on genome-scale models. Further, we show that the pathways produced are biochemically meaningful by an example involving the biosynthesis of inosine 5'-monophosphate (IMP). In particular, the method is able to avoid typical problems associated with graph-theoretic approaches such as the need to define side metabolites or pathways not carrying any net carbon flux appearing in results. Finally, we discuss an application involving reconstruction of amino acid pathways of a recently sequenced organism demonstrating how measurement data can be easily incorporated into ReTrace analysis. ReTrace is licensed under GPL and is freely available for academic use at http://www.cs.helsinki.fi/group/sysfys/software/retrace/.

Conclusion: ReTrace is a useful method in metabolic path finding tasks, combining some of the best aspects in constraint-based and graph-theoretic methods. It finds use in a multitude of tasks ranging from metabolic engineering to metabolic reconstruction of recently sequenced organisms.

Figure 1

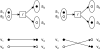
Example atom mappings. Example reaction r: m₁ → m₂ + m₃, two alternative atom mappings Γ₁(r) = {(a₁, a₃), (a₂, a₄)} (left) and Γ₂(r) = {(a₁, a₄), (a₂, a₃)} (right) and corresponding atom graphs G({r}) for atom mappings Γ₁, Γ₂. Atom mappings indicated by shading of atoms. The reaction consumes atoms (r) = {a₁, a₂} and produces atoms (r) = {a₃, a₄}.

Figure 2

Example pathway of three reactions. Example pathway of three reactions r₁, r₂ and r₃ and seven metabolites m₁,..., m₇ containing 13 atoms in total. Atom coloring indicates how the atoms are mapped in reactions. For instance, the pathway transfers atom a₁ to atoms f_P ({a₁}) = {a₅, a₇, a₁₂} and atom a₈ to atom f_P ({a₈}) = {a₁₃}.

Figure 3

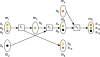
Pathway examples. Examples of four pathways and associated Z_O scores. Assignment of sets S and T are indicated with dashed boxes and atom mappings with atom colorings in figure. Top left: pathway P₁ = {r₁, r₂} transfers all three atoms in S to T, achieving Z_O (P₁, S, T) = = 1. Bottom left: pathway P₂ = {r₃, r₄} transfers green and black atoms to T. Since grey atom is not in S, Z_O (P₂, S, T) = . Top right: branching pathway P₃ = {r₅, r₆, r₇, r₈} transfers all atoms in S, resulting in Z_O (P₃, S, T) = 1. Bottom right: pathway P₄ = {r₉, r₁₀} transfers the only target atom from S, giving Z_O(P₄, S, T) = 1. However, two atoms of S are not transferred to T.

Figure 4

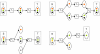
Reduction of Minimum-Set-Cover to Find-Minimal-Pathway. Left: a minimal set cover instance with = {s₁, ..., s₆} (circles) and subset collection = {C₁, C₂, C₃, C₄}. Right: Find-Minimal-Pathway instance corresponding to the set cover instance with 12 atoms and four reactions. Arrows denote mapping of atoms Γ over reactions. In particular, mappings shown with similarly dashed arrow lines belong to the same reaction. Source and target atom sets indicated with S and T.

Figure 5

Reaction and metabolite junctions. Top left: atoms in metabolites m₁ and m₂ are transferred to atoms in metabolite m₅ via two reaction paths p₁ = (r₁, r₃) and p₂ = (r₂, r₃) (indicated by dashed arrows). The paths merge in reaction r₃. Pathway P consisting of reactions r₁, r₂, r₃ has Z_O (P, S, T) = 1, when atoms of {m₁, m₂} and {m₅} comprise the source and target sets S and T, respectively. Top right: pathway P' = {r₁, r₂, r₃} achieves Z_O (P', S, T) = 1 assuming source and target atoms to be all atoms in {m₁, m₂} and {m₄}, respectively. 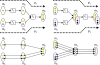The two reaction paths transferring the atoms, = (r₁, r₃) and = (r₂, r₃) merge in metabolite m₃. Subsequently, atoms from m₁ and m₂ are never transferred to the same instance of metabolite m₃ via these paths. Bottom left and right: atom graph representations of pathways P (left) and P' (right). Hollow circles denote atoms which can originate from atoms in metabolites m₁ or m₂.

Figure 6

ReTrace example run. Example ReTrace run for query m₁ → m₁₀ with k = 3 in a database of 9 reactions and 10 metabolites. Atoms numbered from top to bottom as shown in figure. Dashed arrows indicate edges connecting v_Δ and v_U to atom nodes. Otherwise atom graph edges are not drawn; instead, arrows indicate substrates and products in reactions and atoms are mapped in linear fashion. For example, in reaction r₉, atom nodes v_7,1, v_8,1 and v_8,2 are connected to nodes v_9,1, v_9,2 and v_9,3, respectively. At first, U = {m_10,1, m_10,2, m_10,3} are the unresolved nodes. Top: algorithm state after first call to Procedure FindPath. 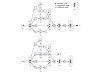The three shortest atom paths found are = (v_Δ, v_1,1, v_8,1, v_9,2, v_10,2, v_U), = (v_Δ, v_1,2, v_8,2, v_9,3, v_10,3, v_U) and = (v_Δ, v_1,2, v_4,2, v_7,1, v_9,1, v_10,1, v_U), with path length ties broken arbitrarily. Choosing to process first, the reaction set corresponding to the atom path is P' = {r₃, r₈, r₉}. Tracing back from v_U, ReTrace finds that v_10,2 and v_10,3 can be traced back to v_Δ, while v_7,1 is added to U. Procedure FindPath is then called recursively. Bottom: algorithm state after second call to Procedure FindPath. Edges to v_U are updated to reflect U = {v_7,1}. Shortest paths from v_Δ to v_U are computed. However, only two paths are found: = (v_Δ, v_1,2, v_4,2, v_7,1, v_U) and = (v_Δ, v_1,2, v_3,1, v_7,1, v_U). Choosing arbitrarily to process next, ReTrace finds out that the reaction set P' = {r₂, r₆} resolves the remaining atom in U and a complete pathway {r₂, r₃, r₆, r₈, r₉} has been discovered.

Figure 7

Excerpt from ReTrace result page. Excerpt from a html result page showing the first pathway found for the query from erythrose 4-phosphate (E4P) and phosphoenolpyruvate (PEP) to phenylalanine (Phe). Green circles in molecule structures indicate atoms in sources that the pathway transfers to target atoms. Additionally, the Z_O score (Z) and the composite map of this pathway are shown.

Figure 8

Result pathway diagram. Diagram of a result pathway for a query from erythrose 4-phosphate (E4P) and phosphoenolpyruvate (PEP) to phenylalanine (Phe). Source and target metabolites are drawn in green and yellow, respectively. For clarity, pathway has been split into two parts, with 5-O-(1-Carboxyvinyl)-3-phosphoshikimate repeated in both parts.

Figure 9

Component sizes and numbers in atom graph. Component size vs. the number of components in the atom graph induced by 7781 KEGG reactions. Components of carbon, nitrogen and phosphorus atoms shown separately. Both X- and Y-axes are shown in log-scale.

Figure 10

Pairwise shortest distances in atom graph. Pairwise distances in three subgraphs corresponding to the carbon, nitrogen and phosphorus specific mappings in the atom graph. Y-axis shown in log-scale.

Figure 11

Distances in atom graph from Acetyl-CoA. Left: Structure and atom numbering of acetyl-CoA. Right: distances in the atom graph from acetyl-CoA carbon atoms 3, 7, 13, 41, 49 and 50. Acetyl carbons 49 and 50 display significantly shorter graph distances compared to other carbons.

Figure 12

ReTrace running time and number of pathways found. Total running time and the number of pathways found in pairwise pathway queries between 13 metabolites. X-axis shows the number of shortest paths searched at each search level. Each point represents averages over 240 pairwise pathway queries.

Figure 13

Metabolite-specific computation time. Total computation time shown separately for each target metabolite. X-axis shows the number of shortest paths searched at the first and second search level. Each point represents queries from 12 metabolites to the target metabolite.

Figure 14

Number of pathways found. Number of pathways found on the average for queries where each metabolite in turn was considered as the source (Y-axis) and target (X-axis). Each point corresponds to averages over 12 results.

Figure 15

Pathway sizes. The average result pathway sizes for queries where each metabolite in turn was considered as the source (Y-axis) and target (X-axis). Each point corresponds to averages over 12 results.

Figure 16

Z_O score distribution in pathways found. Left: Distribution of Z_O score in pathways found for query glucose → IMP. Right: Distribution of pathway sizes. Green bars show the distribution of complete (Z_O = 1) pathways.

Figure 17

Representative result pathway for query glucose → IMP. A representative result pathway for the query glucose → IMP which utilizes reactions commonly used in other result pathways. Glucose and IMP are color-coded green and yellow, respectively.