Spatial and temporal features of synaptic to discharge receptive field transformation in cat area 17
- PMID: 19906874
- PMCID: PMC2822677
- DOI: 10.1152/jn.90946.2008
Spatial and temporal features of synaptic to discharge receptive field transformation in cat area 17
Abstract
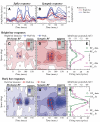
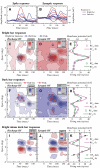
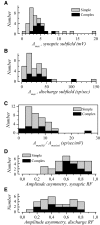
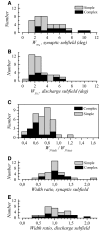
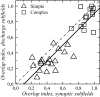
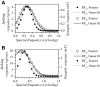
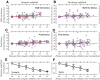
The aim of the present study was to characterize the spatial and temporal features of synaptic and discharge receptive fields (RFs), and to quantify their relationships, in cat area 17. For this purpose, neurons were recorded intracellularly while high-frequency flashing bars were used to generate RFs maps for synaptic and spiking responses. Comparison of the maps shows that some features of the discharge RFs depended strongly on those of the synaptic RFs, whereas others were less dependent. Spiking RF duration depended poorly and spiking RF amplitude depended moderately on those of the underlying synaptic RFs. At the other extreme, the optimal spatial frequency and phase of the discharge RFs in simple cells were almost entirely inherited from those of the synaptic RFs. Subfield width, in both simple and complex cells, was less for spiking responses compared with synaptic responses, but synaptic to discharge width ratio was relatively variable from cell to cell. When considering the whole RF of simple cells, additional variability in width ratio resulted from the presence of additional synaptic subfields that remained subthreshold. Due to these additional, subthreshold subfields, spatial frequency tuning predicted from synaptic RFs appears sharper than that predicted from spiking RFs. Excitatory subfield overlap in spiking RFs was well predicted by subfield overlap at the synaptic level. When examined in different regions of the RF, latencies appeared to be quite variable, but this variability showed negligible dependence on distance from the RF center. Nevertheless, spiking response latency faithfully reflected synaptic response latency.
Figures


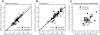
Similar articles
-
Spatial dynamics of receptive fields in cat primary visual cortex related to the temporal structure of thalamocortical feedforward activity. Experiments and models.Exp Brain Res. 2002 Jun;144(4):430-44. doi: 10.1007/s00221-002-1061-5. Epub 2002 Apr 13. Exp Brain Res. 2002. PMID: 12037629
-
Model circuit of spiking neurons generating directional selectivity in simple cells.J Neurophysiol. 1996 Apr;75(4):1515-45. doi: 10.1152/jn.1996.75.4.1515. J Neurophysiol. 1996. PMID: 8727395
-
Dynamics of receptive field size in primary visual cortex.J Neurophysiol. 2007 Jan;97(1):407-14. doi: 10.1152/jn.00830.2006. Epub 2006 Oct 4. J Neurophysiol. 2007. PMID: 17021020
-
Activity-dependent regulation of 'on' and 'off' responses in cat visual cortical receptive fields.J Physiol. 1998 Apr 15;508 ( Pt 2)(Pt 2):523-48. doi: 10.1111/j.1469-7793.1998.00523.x. J Physiol. 1998. PMID: 9508815 Free PMC article.
-
Circuits that build visual cortical receptive fields.Trends Neurosci. 2006 Jan;29(1):30-9. doi: 10.1016/j.tins.2005.11.001. Epub 2005 Nov 23. Trends Neurosci. 2006. PMID: 16309753 Review.
Cited by
-
The mechanism of orientation selectivity in primary visual cortex without a functional map.J Neurosci. 2012 Mar 21;32(12):4049-64. doi: 10.1523/JNEUROSCI.6284-11.2012. J Neurosci. 2012. PMID: 22442071 Free PMC article.
-
Multisensory integration in neurons of the medial pulvinar of macaque monkey.Cereb Cortex. 2023 Apr 4;33(8):4202-4215. doi: 10.1093/cercor/bhac337. Cereb Cortex. 2023. PMID: 36068947 Free PMC article.
-
Inhibition to excitation ratio regulates visual system responses and behavior in vivo.J Neurophysiol. 2011 Nov;106(5):2285-302. doi: 10.1152/jn.00641.2011. Epub 2011 Jul 27. J Neurophysiol. 2011. PMID: 21795628 Free PMC article.
-
Spectrotemporal dynamics of auditory cortical synaptic receptive field plasticity.Hear Res. 2011 Sep;279(1-2):149-61. doi: 10.1016/j.heares.2011.03.005. Epub 2011 Mar 21. Hear Res. 2011. PMID: 21426927 Free PMC article. Review.
-
The accuracy of membrane potential reconstruction based on spiking receptive fields.J Neurophysiol. 2012 Apr;107(8):2143-53. doi: 10.1152/jn.01176.2011. Epub 2012 Jan 25. J Neurophysiol. 2012. PMID: 22279194 Free PMC article.
References
-
- Albus K. A quantitative study of the projection area of the central and the paracentral visual field in area 17 of the cat. I. The precision of the topography. Exp Brain Res 24: 159–179, 1975 - PubMed
-
- Alonso JM, Martinez LM. Functional connectivity between simple cells and complex cells in cat striate cortex. Nat Neurosci 1: 395–403, 1998 - PubMed
-
- Anderson JS, Lampl I, Gillespie DC, Ferster D. The contribution of noise to contrast invariance of orientation tuning in cat visual cortex. Science 290: 1968–1972, 2000 - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

