Composite likelihood estimation of demographic parameters

Abstract

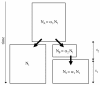
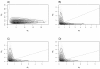
Background: Most existing likelihood-based methods for fitting historical demographic models to DNA sequence polymorphism data to do not scale feasibly up to the level of whole-genome data sets. Computational economies can be achieved by incorporating two forms of pseudo-likelihood: composite and approximate likelihood methods. Composite likelihood enables scaling up to large data sets because it takes the product of marginal likelihoods as an estimator of the likelihood of the complete data set. This approach is especially useful when a large number of genomic regions constitutes the data set. Additionally, approximate likelihood methods can reduce the dimensionality of the data by summarizing the information in the original data by either a sufficient statistic, or a set of statistics. Both composite and approximate likelihood methods hold promise for analyzing large data sets or for use in situations where the underlying demographic model is complex and has many parameters. This paper considers a simple demographic model of allopatric divergence between two populations, in which one of the population is hypothesized to have experienced a founder event, or population bottleneck. A large resequencing data set from human populations is summarized by the joint frequency spectrum, which is a matrix of the genomic frequency spectrum of derived base frequencies in two populations. A Bayesian Metropolis-coupled Markov chain Monte Carlo (MCMCMC) method for parameter estimation is developed that uses both composite and likelihood methods and is applied to the three different pairwise combinations of the human population resequence data. The accuracy of the method is also tested on data sets sampled from a simulated population model with known parameters.

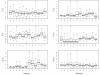
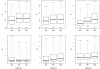
Results: The Bayesian MCMCMC method also estimates the ratio of effective population size for the X chromosome versus that of the autosomes. The method is shown to estimate, with reasonable accuracy, demographic parameters from three simulated data sets that vary in the magnitude of a founder event and a skew in the effective population size of the X chromosome relative to the autosomes. The behavior of the Markov chain is also examined and shown to convergence to its stationary distribution, while also showing high levels of parameter mixing. The analysis of three pairwise comparisons of sub-Saharan African human populations with non-African human populations do not provide unequivocal support for a strong non-African founder event from these nuclear data. The estimates do however suggest a skew in the ratio of X chromosome to autosome effective population size that is greater than one. However in all three cases, the 95% highest posterior density interval for this ratio does include three-fourths, the value expected under an equal breeding sex ratio.

Conclusion: The implementation of composite and approximate likelihood methods in a framework that includes MCMCMC demographic parameter estimation shows great promise for being flexible and computationally efficient enough to scale up to the level of whole-genome polymorphism and divergence analysis. Further work must be done to characterize the effects of the assumption of linkage equilibrium among genomic regions that is crucial to the validity of applying the composite likelihood method.

Figure 1

Demographic model. A schematic of the two population divergence model that is fit to the joint frequency spectrum. Looking forward in time, the ancestral population splits t₁ + t₂ generations before the present into two descendant populations. At this time, the effective size of population 1 is assumed to be N₁ and the founding size of population 2 is assumed to be α₂N₁. Then, after t₂ generations, population 2 grows to effective size α₁N₁. Lastly, the effective size of the common ancestral population is assumed to be α₃N₁. Thus, the divergence model is governed by five parameters that need to estimated: t₁, t₂, α₁, α₂ and α₃.

Figure 2

Simulated data estimates. Accuracy of parameter estimation for the twelve parameters in the divergence model. For each parameter, the ratio of the estimated median posterior probability to the "true" value of the parameter in the simulation. The horizontal gray lines delineate a ratio of unity. The heavy lines in the box plots are the median, the hinge of the boxes are the 25% and 75% quantiles and the outer whiskers represent the 2.5% and 97.5% quantiles. Results are presented for each of the twelve simulated datasets, the parameters of which are listed in Table 1. Posterior probability distributions are taken over all ten replicate runs of the Markov chain.

Figure 3

Human data estimates. Representations of the posterior probability distributions for the six divergence model parameters from the data of Wall et al. [14]. Three pairwise population comparisons are plotted: Africa-Asia (AA), Africa-Europe (AE), and Africa-Oceania (AO). The heavy lines in the box plots are the median, the hinge of the boxes are the 25% and 75% quantiles and the outer whiskers represent the 2.5% and 97.5% quantiles. Numerical values for the median and 95% highest posterior density intervals can be found in Table 3. In the plot of the ratio of the X chromosome to autosomal effective population size (h), the horizontal gray line delineates a ratio of 3/4. As in Figure 2, the posterior probability distributions shown here are taken over all ten replicate runs of the Markov chain.

Figure 4

Evidence for population growth. Joint posterior density plots for the α₁ and α₂ parameters for four different data sets: A) simulated data set A, B) Africa-Asia, C) Africa-Europe, and D) Africa-Oceania. The dashed line plots the case of α₁ = α₂, which is indicative of no recent population growth. In panel A, the posterior density for the simulated bottleneck data lies below the dashed line, supporting recent population growth. However, in the other three panels representing the empirical resequence data of [14], the joint posterior density lies within the one-to-one region, suggesting a lack of evidence for recent population growth.