Probabilistic model of microbial cell growth, division, and mortality

Abstract

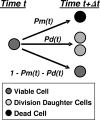
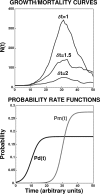
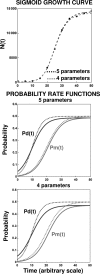
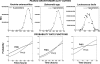
After a short time interval of length deltat during microbial growth, an individual cell can be found to be divided with probability Pd(t)deltat, dead with probability Pm(t)deltat, or alive but undivided with the probability 1-[Pd(t)+Pm(t)]deltat, where t is time, Pd(t) expresses the probability of division for an individual cell per unit of time, and Pm(t) expresses the probability of mortality per unit of time. These probabilities may change with the state of the population and the habitat's properties and are therefore functions of time. This scenario translates into a model that is presented in stochastic and deterministic versions. The first, a stochastic process model, monitors the fates of individual cells and determines cell numbers. It is particularly suitable for small populations such as those that may exist in the case of casual contamination of a food by a pathogen. The second, which can be regarded as a large-population limit of the stochastic model, is a continuous mathematical expression that describes the population's size as a function of time. It is suitable for large microbial populations such as those present in unprocessed foods. Exponential or logistic growth with or without lag, inactivation with or without a "shoulder," and transitions between growth and inactivation are all manifestations of the underlying probability structure of the model. With temperature-dependent parameters, the model can be used to simulate nonisothermal growth and inactivation patterns. The same concept applies to other factors that promote or inhibit microorganisms, such as pH and the presence of antimicrobials, etc. With Pd(t) and Pm(t) in the form of logistic functions, the model can simulate all commonly observed growth/mortality patterns. Estimates of the changing probability parameters can be obtained with both the stochastic and deterministic versions of the model, as demonstrated with simulated data.

FIG. 1.

Cellular events from which the quasichemical model of microbial growth and mortality has been derived. Data are from Doona et al. (12).

FIG. 2.

Cellular events from which the probabilistic model of microbial growth and mortality has been derived.

FIG. 3.

Microbial population dynamics at the cellular level.

FIG. 4.

Simulated isothermal microbial growth curves generated with the same deterministic continuous model (equation 14) and their corresponding division and mortality probability functions, P_d(t) and P_m(t), respectively. (Left) Growth curve with noticeable lag; (middle) growth without lag; (right) noticeable lag followed by a growth peak and intensive mortality. Notice that these very distinct growth patterns are all a manifestation of different relationships between underlying probability functions.

FIG. 5.

Simulated isothermal microbial survival (inactivation) curves generated with the deterministic continuous model (equation 14) plotted on linear and semilogarithmic coordinates. Also shown are the corresponding division and mortality probability functions, P_d(t) and P_m(t), respectively. (Left) Log-linear survival curve; (middle) curve with a flat shoulder; (right) inactivation followed by resumed growth. Notice that the different patterns were all produced with the same model (equation 14), which produced the growth curves shown in Fig. 4.

FIG. 6.

Simulated growth curves generated with the discrete (stochastic) version of the model with the same underlying division and mortality probability functions but different δt's. Notice the curves' increased smoothness as δt decreases and N(t) increases.

FIG. 7.

Simulated growth curves started from a single cell generated with the discrete (stochastic) version of the model (equation 4), with different underlying division and mortality probability functions (top), and life histories of 50 such cells (bottom). (A) Growth with lag; (B) growth with no lag; (C) peaked growth with lag. Notice the jagged appearance of the curves.

FIG. 8.

Simulated growth curves started from a single group of 10 cells generated with the discrete (stochastic) version of the model (equation 4), with different underlying division and mortality probability functions (top), and life histories of 50 such groups of 10 (bottom). (A) Growth with lag; (B) growth with no lag; (C) peaked growth with lag. Notice that all the growth curves appear less jagged than those for the individual cells shown in Fig. 7.

FIG. 9.

Simulated growth curves started from a single group of 100 cells generated with the discrete (stochastic) version of the model (equation 4), with different underlying division and mortality probability functions (top), and life histories of 50 such groups of 100 (bottom). (A) Growth with lag; (B) growth with no lag; (C) peaked growth with lag. Notice that all the growth curves are smooth in comparison with those for the individual cells and smaller groups shown in Fig. 7 and 8, respectively.

FIG. 10.

Extraction of the division and mortality probability functions from simulated sigmoid growth data with small scatter. (Top) Fit of the four- and five-parameter versions of equation 16; (middle and bottom) corresponding probability functions calculated with the regression parameters (solid lines) and those used to create the data (dashed lines). Notice the similarity between the division and mortality probability functions estimated by the four- and five-parameter deterministic models (equations 15 and 16, respectively). The parameters for the shown data points’ generation and the retrieved parameters are listed in Table 1.

FIG. 11.

Extraction of the division and mortality probability functions from a simulated peaked growth curve. (Top) Fit of the five-parameter version of equation 16; (bottom) corresponding probability functions calculated with the regression parameters (solid lines) and those used to create the data (dashed lines). The parameters for the shown data points’ generation and the retrieved parameters are listed in Table 1.

FIG. 12.

Experimental sigmoid growth curves for E. coli O157:H7, Salmonella spp., and Y. enterocolitica fitted with the four- and five-parameter versions of equation 16 as a model (top) and the corresponding estimated underlying division and mortality probability functions (bottom). The experimental data are from Koseki and Isobe (18) and the Food Standard Agency (http://combase.arserrc.gov/; record numbers B124_39 and B002_146), respectively.

FIG. 13.

Experimental peaked growth/mortality curves for Y. enterocolitica, Salmonella spp., and L. lactis fitted with the five-parameter version of equation 16 as a model (top) and the corresponding estimated underlying division and mortality probability functions (bottom). The experimental data are from the Food Standard Agency (http://combase.arserrc.gov/; record numbers B092_4 and B002_92) and Dougherty et al. (13), respectively.