Analysis of couch position tolerance limits to detect mistakes in patient setup

Abstract

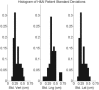
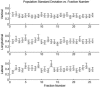
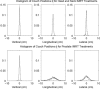
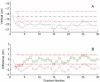
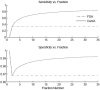
This work investigates the use of the tolerance limits on the treatment couch position to detect mistakes in patient positioning and warn users of possible treatment errors. Computer controlled radiotherapy systems use the position of the treatment couch as a surrogate for patient position and a tolerance limit is applied against a planned position. When the couch is out of tolerance a warning is sent to a user to indicate a possible mistake in setup. A tight tolerance may catch all positioning mistakes while as the same time sending too many warnings; while a loose tolerance will not catch all mistakes. We develop a statistical model of the absolute position for the three translational axes of the couch. The couch position for any fraction is considered a random variable x(i). The ideal planned couch position x(p) is unknown before a patient starts treatment and must be estimated from the daily positions x(i). As such x(p) is also a random variable. The tolerance, tol, is applied to the difference between the daily and planned position, d(i) = x(i) - x(p). The di is a linear combination of random variables and therefore the density of di is the convolution of distributions of xi and xp. Tolerance limits are based on the standard deviation of d(i) such that couch positions that are more than 2 standard deviation away are considered out of tolerance. Using this framework we investigate two methods of setting x(p) and tolerance limits. The first, called first day acquire (FDA), is to take couch position on the first day as the planned position. The second is to use the cumulative average (CumA) over previous fractions as the planned position. The standard deviation of d(i) shrinks as more samples are used to determine x(p) and so the tolerance limit shrinks as a function of fraction number when a CumA technique is used. The metrics of sensitivity and specificity were used to characterize the performance of the two methods to correctly identify a couch position as in or out of tolerance. These two methods were tested using simulated and real patient data. Five clinical sites with different indexed immobilization were tested. These were whole brain, head and neck, breast, thorax and prostate. Analysis of the head and neck data shows that it is reasonable to model the daily couch position as a random variable in this treatment site. Using an average couch position for x(p) increased the sensitivity of the couch interlock and reduced the chances of acquiring a couch position that was a statistical outlier. Analysis of variation in couch position for different sites allowed the tolerance limit to be set specifically for a site and immobilization device. The CumA technique was able to increase the sensitivity of detecting out of tolerance positions while shrinking tolerance limits for a treatment course. Making better use of the software interlock on the couch positions could have a positive impact on patient safety and reduce mistakes in treatment delivery.

Figure 1

Histograms of the standard deviation of each H&N patient's digital couch coordinates over the course of their treatment.

Figure 2

Graph of the population standard deviation of H&N treatment couch positions on a treatment fraction basis with corresponding 95% confidence intervals. All patients had at least 26 fractions treated. No trend can be seen in the data to indicate that any fraction has more or less variation than another.

Figure 3

Histogram of couch positions after the average of each patient has been subtracted, $d_i=x_i-\mu$. The H&N IMRT patients are shown in the top row; the prostate IMRT patients in the bottom row. Both of these treatment sites used daily image guidance to remove systematic and random errors in the target position. The large differences between the two sites are due to the high level of index immobilization used in H&N and no immobilization used for prostate cases.

Figure 4

Graphs of table vertical coordinates and differences for a selected patient. Graph A shows the absolute coordinate of the couch (blue) where the couch positions more than $2{\sigma }_{\mathit{\text{pop}}}$ from the mean are marked with a red diamond and are considered to be out of tolerance. The planned couch position is shown in black, with the FDA method as a broken line and the CumA method as a solid line. The tolerance limit is show as a red broken line. Graph B shows the same data, but plots the difference from the planned values. The CumA technique is plotted to indicate positions marked as out of tolerance (red squares) and within tolerance (green squares). The FDA technique is plotted with circles.

Figure 5

Graph of the sensitivity and specificity for the FDA (broken line) and CumA (solid line) techniques as a function of fraction number for simulated data. The two techniques are equivalent for the first two fractions. The CumA technique shows improvement in the ability to detect which couch positions are out of tolerance.