Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2009 Oct;36(10):4625-33.
doi: 10.1118/1.3218761.

Sliding characteristic and material compressibility of human lung: parametric study and verification

A Al-Mayah  1 , J Moseley, M Velec, K K Brock
Affiliations

Sliding characteristic and material compressibility of human lung: parametric study and verification

A Al-Mayah et al. Med Phys. 2009 Oct.

Abstract

Purpose: To find and verify the optimum sliding characteristics and material compressibility that provide the minimum error in deformable image registration of the lungs.

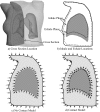
Methods: A deformable image registration study has been conducted on a total of 16 lung cancer patients. Patient specific three dimensional finite element models have been developed to model left and right lungs, chest (body), and tumor based on 4D CT images. Contact surfaces have been applied to lung-chest cavity interfaces. Experimental test data are used to model nonlinear material properties of lungs. A parametric study is carried out on seven patients, 20 conditions for each, to investigate the sliding behavior and the tissue compressibility of lungs. Three values of coefficient of friction of 0, 0.1, and 0.2 are investigated to model lubrication and sliding restriction on the lung-chest cavity interface. The effect of material compressibility of lungs is studied using Poisson's ratios of 0.35, 0.4, 0.45, and 0.499. The model accuracy is examined by calculating the difference between the image-based displacement of bronchial bifurcation points identified in the lung images and the calculated corresponding model-based displacement. Furthermore, additional bifurcation points around the tumor and its center of mass are used to examine the effect of the mentioned parameters on the tumor localization.

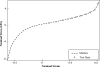
Results: The frictionless contact model with 0.4 Poisson's ratio provides the smallest residual errors of 1.1 +/- 0.9, 1.5 +/- 1.3, and 2.1 +/- 1.6 mm in the LR, AP, and SI directions, respectively. Similarly, this optimum model provides the most accurate location of the tumor with residual errors of 1.0 +/- 0.6, 0.9 +/- 0.7, and 1.4 +/- 1.0 mm in all three directions. The accuracy of this model is verified on an additional nine patients with average errors of 0.8 +/- 0.7, 1.3 +/- 1.1, and 1.7 +/- 1.6 mm in the LR, AP, and SI directions, respectively.

Conclusions: The optimum biomechanical model with the smallest registration error is when frictionless contact model and 0.4 Poisson's ratio are applied. The overall accuracies of all bifurcation points in all 16 patients including tumor points are 1.0 +/- 0.7, 1.2 +/- 1.0, and 1.7 +/- 1.4 mm in the LR, AP, and SI directions, respectively.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Model components including body, lungs, and tumor.
Figure 2
Figure 2
Boundary conditions on (a) a model cross section where (b) the geometry differences between inhale and exhale phases are applied in a form of displacements to the body and chest cavity. In the model without the contact surface (c) these displacements are applied to the lung’s nodes directly since they are attached to those of the chest cavities. However, in the contact model (d) the boundary conditions are applied to the chest cavity nodes, not to the lungs, allowing sliding of lungs inside chest cavities. Note: The gap between the lung and chest cavity in (d) is magnified for the sake of clarity.
Figure 3
Figure 3
Experimental test data of human lung tissue represented by a nominal stess-strain relationship. The data are verified using the Marlow model for hyperelastic material properties.
Figure 4
Figure 4
Average bifurcation displacement in the seven patients of the parametric study.
See this image and copyright information in PMC

References

    1. Kessler M. L., “Image registration and data fusion in radiation therapy,” Br. J. Radiol. BJRAAP 79, S99–S108 (2006).10.1259/bjr/70617164 - DOI - PubMed
    1. Crum W. R., Hartkens T., and Hill D. L. G., “Non-rigid image registration: Theory and practice,” Br. J. Radiol. BJRAAP 77, S140–S153 (2004).10.1259/bjr/25329214 - DOI - PubMed
    1. Maintz J. B. A. and Viergever M. A., “A survey of medical image registration,” Med. Image Anal. MIAECY 2, 1–36 (1998).10.1016/S1361-8415(01)80026-8 - DOI - PubMed
    1. Holden K., “A review of geometric transformations for nonrigid body registration,” IEEE Trans. Med. Imaging ITMID4 27, 111–128 (2008).10.1109/TMI.2007.904691 - DOI - PubMed
    1. Carter T. J., Sermesant M., Cash D. M., Barratt D. C., Tanner C., and Hawkes D. J., “Application of soft tissue modelling to image-guided surgery,” Med. Eng. Phys. MEPHEO 27, 893–909 (2005).10.1016/j.medengphy.2005.10.005 - DOI - PubMed

Publication types