Internal models and neural computation in the vestibular system
- PMID: 19937232
- PMCID: PMC2853943
- DOI: 10.1007/s00221-009-2054-4
Internal models and neural computation in the vestibular system
Abstract
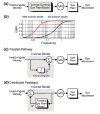
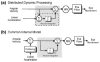
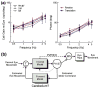
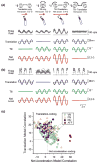
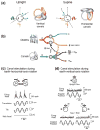
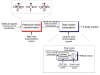
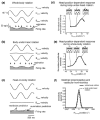
The vestibular system is vital for motor control and spatial self-motion perception. Afferents from the otolith organs and the semicircular canals converge with optokinetic, somatosensory and motor-related signals in the vestibular nuclei, which are reciprocally interconnected with the vestibulocerebellar cortex and deep cerebellar nuclei. Here, we review the properties of the many cell types in the vestibular nuclei, as well as some fundamental computations implemented within this brainstem-cerebellar circuitry. These include the sensorimotor transformations for reflex generation, the neural computations for inertial motion estimation, the distinction between active and passive head movements, as well as the integration of vestibular and proprioceptive information for body motion estimation. A common theme in the solution to such computational problems is the concept of internal models and their neural implementation. Recent studies have shed new insights into important organizational principles that closely resemble those proposed for other sensorimotor systems, where their neural basis has often been more difficult to identify. As such, the vestibular system provides an excellent model to explore common neural processing strategies relevant both for reflexive and for goal-directed, voluntary movement as well as perception.
Figures


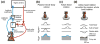
References
-
- Ajemian R, Green A, Bullock D, Sergio L, Kalaska J, Grossberg S. Assessing the function of motor cortex: single-neuron models of how neural response is modulated by limb biomechanics. Neuron. 2008;58:414–428. - PubMed
-
- Allum JH, Honegger F. Interactions between vestibular and proprioceptive inputs triggering and modulating human balance-correcting responses differ across muscles. Exp Brain Res. 1998;121:478–494. - PubMed
-
- Angelaki DE. Three-dimensional organization of otolith-ocular reflexes in rhesus monkeys. III. Responses to translation. J Neurophysiol. 1998;80:680–695. - PubMed
-
- Angelaki DE. Eyes on target: what neurons must do for the vestibuloocular reflex during linear motion. J Neurophysiol. 2004;92:20–35. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

