Motor-substrate interactions in mycoplasma motility explains non-Arrhenius temperature dependence

Abstract

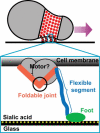
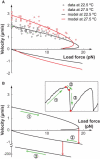
Mycoplasmas exhibit a novel, substrate-dependent gliding motility that is driven by approximately 400 "leg" proteins. The legs interact with the substrate and transmit the forces generated by an assembly of ATPase motors. The velocity of the cell increases linearly by nearly 10-fold over a narrow temperature range of 10-40 degrees C. This corresponds to an Arrhenius factor that decreases from approximately 45 k(B)T at 10 degrees C to approximately 10 k(B)T at 40 degrees C. On the other hand, load-velocity curves at different temperatures extrapolate to nearly the same stall force, suggesting a temperature-insensitive force-generation mechanism near stall. In this article, we propose a leg-substrate interaction mechanism that explains the intriguing temperature sensitivity of this motility. The large Arrhenius factor at low temperature comes about from the addition of many smaller energy barriers arising from many substrate-binding sites at the distal end of the leg protein. The Arrhenius dependence attenuates at high temperature due to two factors: 1), the reduced effective multiplicity of energy barriers intrinsic to the multiple-site binding mechanism; and 2), the temperature-sensitive weakly facilitated leg release that curtails the power stroke. The model suggests an explanation for the similar steep, sub-Arrhenius temperature-velocity curves observed in many molecular motors, such as kinesin and myosin, wherein the temperature behavior is dominated not by the catalytic biochemistry, but by the motor-substrate interaction.

Figure 1

Motility apparatus of M. mobile. Four-hundred leg proteins are located at the neck of the M. mobile cell. Each leg assumes a music-note-like shape (zoom-in view), with two arms at the proximal end, and a long flexible segment (blue) with a foot (green) that interacts with the substrate.

Figure 2

Mechanochemical model of a single leg protein. (A) Mechanochemical cycle of the leg. The leg starts in the front conformation with the foot bound to the substrate. As ATP zippers into the catalytic site, the motor carries out a power stroke, pulling the cell forward. After the power stroke, the cell continues moving forward at constant velocity V, driven by the collective action of the other legs. The foot lags behind until the long segment is once again in tension. Acting on one end of the foot, the tension helps peel the foot off the substrate. The system must wait for the foot to release from the substrate so that the leg can reset to the front conformation, allowing the motor to bind ATP once again. The cycle repeats as the foot rebinds to the substrate. ATP binding and foot rebinding are assumed to happen very fast, thus not resolved in the analysis. During the cycle, the power stroke applies a positive force on the cell body, and the foot, tethered beyond its backward restressed position, applies a negative force (blue arrows). (B) Mechanism of foot peeling. The foot interacts with the sialic acids in the substrate through multiple binding sites. The bonds are shown by green projections in the zoom-in view on the right. When the stretched intermediate segment pulls on the foot from one end, most of the tension is exerted on the frontmost bond and thus significantly facilitates its unbinding, analogous to peeling-off a Velcro strip. In the idealized case, the bonds break off sequentially, forming a Markov process as shown in the sequence of events on the right. The Markov process gives an average peel-off rate of the foot as in Eq. 2.

Figure 3

Temperature-velocity results. (A) Temperature versus velocity curve. Circles and error bars show the experiment data (taken from Miyata et al. (23)); the dashed line is the fitting of the model without weakly facilitated foot release during the power stroke using Eq. 1; the solid line shows the result with weakly facilitated foot release during power stroke using Eq. 3. The effect of weakly facilitated foot release becomes significant at high temperatures, and corrects the deviation from the data. (B) The Arrhenius plots of the foot rates and of the data. For comparison, the rates have been multiplied by corresponding constants to level the logarithm plots at the left end. The whole foot peel-off rate, R_p, has a much larger Arrhenius factor than the off-rate of a single site does because of the multiplying effect shown in Eq. 2. Also, the Arrhenius factor of R_p decreases as temperature increases. (C) The peel-off rate R_p and weakly facilitated release rate R_wf. The weakly facilitated rate becomes significant at ∼25°C, resulting in the attenuation of velocity at high temperatures.

Figure 4

Load-velocity curve explains the dynamical behavior in the laser trap experiments. (A) Load force versus velocity curve. The model results are computed beyond the velocity regime measured in the experiments. Hysteresis is predicted by the model. (B) Mapping of the dynamical trajectory onto the load-velocity curve. The middle branch of the load-velocity curve is unstable. The straight line added at the bottom of the plot shows the hydrodynamic load-velocity curve, i.e., when the cell is off the substrate. The dynamical trajectory measured from an optically trapped Mycoplasma is shown in the inset (taken from Miyata et al. (23)). The labeled green arrows along the load-velocity curve and the dynamic trajectory show, correspondingly, the three motility phases of the cell: 1), forward; 2), backward; and 3), free after detachment. The red arrows on the load-velocity curve and the red dots on the trajectory indicate corresponding transitions between the three phases. This branching load-velocity curve explains the forward-to-backward transition in the dynamical trajectory. However, the backward-to-break-off transition cannot be explained without further experimental information.

Figure 5

Cycle period and residence times of each stage change with temperature. (A) The cycle period decreases with temperature, ranging between 10 and ∼10² ms in the relevant temperature range. (B) Temperature affects the durations of the power stroke (solid), restretching (dashed), peel-off (dotted), and the unbound states (dash-and-dotted). These results are computed from Eq. S28 in the Supporting Material.

Figure 6

Predictions of the model. (A) The effect of sialic acid concentration on the cell velocity. The horizontal axis shows the logarithm of the single-site binding rate, which is directly related to the density of sialic acid on the substrate surface. The model predicts the existence of an optimal sialic acid density for Mycoplasma motility, to be compared with the experiment result presented in Fig. 6 of Nagai and Miyata (30). (B) The effect of viscosity on the load-velocity curve. The curves are computed for the mediums bearing the normal water viscosity (solid line), 10 times larger (dashed line), and 100 times larger (dotted line). The cell velocity decreases when viscosity increases. In addition, the load-velocity curve becomes more concave with larger viscosity.