Temperature jump induced force generation in rabbit muscle fibres gets faster with shortening and shows a biphasic dependence on velocity
- PMID: 19948657
- PMCID: PMC2825612
- DOI: 10.1113/jphysiol.2009.179200
Temperature jump induced force generation in rabbit muscle fibres gets faster with shortening and shows a biphasic dependence on velocity
Abstract
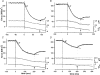
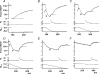
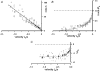
We examined the tension responses to ramp shortening and rapid temperature jump (<0.2 ms, 3-4 degrees C T-jump) in maximally Ca(2+)-activated rabbit psoas muscle fibres at 8-9 degrees C (the fibre length (L(0)) was approximately 1.5 mm and sarcomere length 2.5 microm). The aim was to investigate the strain sensitivity of crossbridge force generation in muscle. The T-jump induced tension rise was examined during steady shortening over a wide range of velocities (V) approaching the V(max) (V range approximately 0.01 to approximately 1.5 L(0) s(1)). In the isometric state, a T-jump induced a biphasic tension rise consisting of a fast (approximately 50 s(1), phase 2b) and a slow (approximately 10 s(1), phase 3) component, but if treated as monophasic the rate was approximately 20 s(1). During steady shortening the T-jump tension rise was monophasic; the rate of tension rise increased linearly with shortening velocity, and near V(max) it was approximately 200 s(1), approximately 10x faster than in the isometric state. Relative to the tension reached after the T-jump, the amplitude increased with shortening velocity, and near V(max) it was 4x larger than in the isometric state. Thus, the temperature sensitivity of muscle force is markedly increased with velocity during steady shortening, as found in steady state experiments. The rate of tension decline during ramp shortening also increased markedly with increase of velocity. The absolute amplitude of T-jump tension rise was larger than that in the isometric state at the low velocities (<0.5 L(0) s(1)) but decreased to below that of the isometric state at the higher velocities. Such a biphasic velocity dependence of the absolute amplitude of T-jump tension rise implies interplay between, at least, two processes that have opposing effects on the tension output as the shortening velocity is increased, probably enhancement of crossbridge force generation and faster (post-stroke) crossbridge detachment by negative strain. Overall, our results show that T-jump force generation is strain sensitive and becomes considerably faster when exposed to negative strain. Thus the crossbridge force generation step in muscle is both temperature sensitive (endothermic) and strain sensitive.
Figures
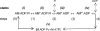


Similar articles
-
Force and power generating mechanism(s) in active muscle as revealed from temperature perturbation studies.J Physiol. 2010 Oct 1;588(Pt 19):3657-70. doi: 10.1113/jphysiol.2010.194001. J Physiol. 2010. PMID: 20660565 Free PMC article. Review.
-
Force generation examined by laser temperature-jumps in shortening and lengthening mammalian (rabbit psoas) muscle fibres.J Physiol. 2007 Nov 15;585(Pt 1):263-77. doi: 10.1113/jphysiol.2007.142208. Epub 2007 Oct 4. J Physiol. 2007. PMID: 17916609 Free PMC article.
-
Endothermic force generation, temperature-jump experiments and effects of increased [MgADP] in rabbit psoas muscle fibres.J Physiol. 2005 Sep 1;567(Pt 2):471-92. doi: 10.1113/jphysiol.2005.090084. Epub 2005 Jun 23. J Physiol. 2005. PMID: 15975981 Free PMC article.
-
An analysis of the temperature dependence of force, during steady shortening at different velocities, in (mammalian) fast muscle fibres.J Muscle Res Cell Motil. 2008;29(1):9-24. doi: 10.1007/s10974-008-9138-9. Epub 2008 Jun 4. J Muscle Res Cell Motil. 2008. PMID: 18523851 Free PMC article.
-
Crossbridge mechanism(s) examined by temperature perturbation studies on muscle.Adv Exp Med Biol. 2010;682:247-66. doi: 10.1007/978-1-4419-6366-6_14. Adv Exp Med Biol. 2010. PMID: 20824530 Review.
Cited by
-
Force and power generating mechanism(s) in active muscle as revealed from temperature perturbation studies.J Physiol. 2010 Oct 1;588(Pt 19):3657-70. doi: 10.1113/jphysiol.2010.194001. J Physiol. 2010. PMID: 20660565 Free PMC article. Review.
-
ATP binding and cross-bridge detachment steps during full Ca²⁺ activation: comparison of myofibril and muscle fibre mechanics by sinusoidal analysis.J Physiol. 2012 Jul 15;590(14):3361-73. doi: 10.1113/jphysiol.2012.228379. Epub 2012 May 14. J Physiol. 2012. PMID: 22586213 Free PMC article.
-
Temperature Effects on Force and Actin⁻Myosin Interaction in Muscle: A Look Back on Some Experimental Findings.Int J Mol Sci. 2018 May 22;19(5):1538. doi: 10.3390/ijms19051538. Int J Mol Sci. 2018. PMID: 29786656 Free PMC article. Review.
-
Crossbridge and filament compliance in muscle: implications for tension generation and lever arm swing.J Muscle Res Cell Motil. 2010 Dec;31(4):245-65. doi: 10.1007/s10974-010-9232-7. Epub 2010 Dec 4. J Muscle Res Cell Motil. 2010. PMID: 21132353 Review.
-
The endothermic ATP hydrolysis and crossbridge attachment steps drive the increase of force with temperature in isometric and shortening muscle.J Physiol. 2015 Apr 15;593(8):1997-2016. doi: 10.1113/jphysiol.2014.284992. Epub 2015 Feb 11. J Physiol. 2015. PMID: 25564737 Free PMC article.
References
-
- Bershitsky SY, Tsaturyan AK. Tension transients initiated by the Joule temperature jump during steady shortening of skinned muscle fibres. In: Maréchal G, Carraro U, editors. Muscle and Motility. Andover, Hampshire: Intercept; 1990. pp. 277–281.
-
- Colombini B, Nocella M, Benelli G, Cecchi G, Bagni MA. Effect of temperature on cross-bridge properties in intact frog muscle fibres. Am J Physiol Cell Physiol. 2008;294:C1113–C1117. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

