The number of beams in IMRT--theoretical investigations and implications for single-arc IMRT

Abstract

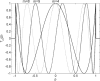
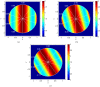
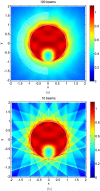
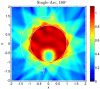
The first purpose of this paper is to shed some new light on the old question of selecting the number of beams in intensity-modulated radiation therapy (IMRT). The second purpose is to illuminate the related issue of discrete static beam angles versus rotational techniques, which has recently re-surfaced due to the advancement of volumetric modulated arc therapy (VMAT). A specific objective is to find analytical expressions that allow one to address the points raised above. To make the problem mathematically tractable, it is assumed that the depth dose is flat and that the lateral dose profile can be approximated by polynomials, specifically Chebyshev polynomials of the first kind, of finite degree. The application of methods known from image reconstruction then allows one to answer the first question above as follows: the required number of beams is determined by the maximum degree of the polynomials used in the approximation of the beam profiles, which is a measure of the dose variability. There is nothing to be gained by using more beams. In realistic cases, in which the variability of the lateral dose profile is restricted in several ways, the required number of beams is of the order of 10-20. The consequence of delivering the beams with a 'leaf sweep' technique during continuous rotation of the gantry, as in VMAT, is also derived in an analytical form. The main effect is that the beams fan out, but the effect near the axis of rotation is small. This result can serve as a theoretical justification of VMAT. Overall the analytical derivations in this paper, albeit based on strong simplifications, provide new insights into, and a deeper understanding of, the beam angle problem in IMRT. The decomposition of the beam profiles into well-behaved and easily deliverable smooth functions, such as Chebyshev polynomials, could be of general interest in IMRT treatment planning.

Figure 1

Examples of Chebyshev polynomials of the first kind, T_m(p), for m = 4 (solid line), m = 8 (dotted line) and m = 9 (dashed = line).

Figure 2

Making rotating beams from fixed beam angles. By varying the weights of intensity-modulated beams from fixed beam directions, one can create beams from arbitrary directions, (a): 0°, (b): 15°, (c): 30°. In every case, five beams from fixed evenly spaced directions (every 36°) are used, as shown by the white lines. Every beam produces a Chebyshev T₄(p) fluence profile but with different weights that are calculated with equation (5) and shown as white numbers next to the beams. Negative values of the fluence profiles are avoided by a zero offset, i.e. by adding constant fluence. See the text for further information.

Figure 3

Dose distributions for the treatment of a circular target volume (white solid line) that `wraps around' a small circular critical structure (white dashed line) with K = 100 beams (a) and K = 10 beams (b). The dose prescription is one dose unit to the target volume, and a dose reduction to 0.5 units is requested in the critical structure. All beams are composed of M = 10 Chebyshev polynomials with degrees between m = 0 and m = 9. Within the target circle, which encompasses the critical structure, the two distributions in (a) and (b) are identical, i.e., there is no benefit in using more than 10 beams here.

Figure 4

The effect of gantry motion during leaf sweep IMRT delivery is illustrated here for one of the ten beams that produce the dose distribution shown in figure 3(b). Specifically, the vertical beam (ϕ₀ = 0°) from that example is considered. The dose from that beam without motion during delivery is shown in (a). Here the beam comes straight from the top. In (b) gantry motion is simulated in the counter-clockwise direction from ϕ = −9° to 9° during leaf sweep IMRT delivery of that beam. The leaves move from the left to the right. In the upper half of part (b) (for positive y), the resulting motion of the field edges in the x-direction is reduced by the gantry motion (retrograde motion), whereas in the lower half (negative y) it is increased (prograde motion). At y = 0 there is no effect of the gantry motion.

Figure 5

Dose distribution that results from delivering the ten beams used in figure 3(b) not from static gantry angles but during continuous gantry motion in the Single-Arc mode. The first of the ten beams is delivered with MLC leaf sweep while the gantry rotates from −9° to 9°, the second during the gantry arc segment from 9° to 27°, and so forth. The total Single-Arc is being delivered over 180°, from −9 to 171°.