Quimp3, an automated pseudopod-tracking algorithm
- PMID: 19949291
- PMCID: PMC2852557
- DOI: 10.4161/cam.4.1.9953
Quimp3, an automated pseudopod-tracking algorithm
Abstract
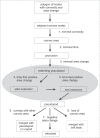
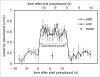
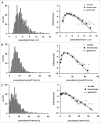
To understand movement of amoeboid cells we have developed an information tool that automatically detects protrusions of moving cells. The algorithm uses digitized cell recordings at a speed of approximately 1 image per second that are analyzed in three steps. In the first part, the outline of a cell is defined as a polygon of approximately 150 nodes, using the previously published Quimp2 program. By comparing the position of the nodes in place and time, each node contains information on position, local curvature and speed of movement. The second part uses rules for curvature and movement to define the position and time of start and end of a growing pseudopod. This part of the algorithm produces quantitative data on size, surface area, lifetime, frequency and direction of pseudopod extension. The third part of the algorithm assigns qualitative properties to each pseudopod. It decides on the origin of a pseudopod as splitting of an existing pseudopod or as extension de novo. It also decides on the fate of each pseudopod as merged with the cell body or retracted. Here we describe the pseudopod tool and present the first data based on the analysis of approximately 1,000 pseudopodia extended by Dictyostelium cells in the absence of external cues.
Figures


Similar articles
-
A model for a correlated random walk based on the ordered extension of pseudopodia.PLoS Comput Biol. 2010 Aug 12;6(8):e1000874. doi: 10.1371/journal.pcbi.1000874. PLoS Comput Biol. 2010. PMID: 20711349 Free PMC article.
-
The ordered extension of pseudopodia by amoeboid cells in the absence of external cues.PLoS One. 2009;4(4):e5253. doi: 10.1371/journal.pone.0005253. Epub 2009 Apr 22. PLoS One. 2009. PMID: 19384419 Free PMC article.
-
Pseudopod Tracking and Statistics During Cell Movement in Buffer and Chemotaxis.Methods Mol Biol. 2024;2828:185-204. doi: 10.1007/978-1-0716-4023-4_14. Methods Mol Biol. 2024. PMID: 39147978
-
Moving forward: mechanisms of chemoattractant gradient sensing.Physiology (Bethesda). 2004 Oct;19:300-8. doi: 10.1152/physiol.00017.2004. Physiology (Bethesda). 2004. PMID: 15381759 Review.
-
Is there a pilot in a pseudopod?Eur J Cell Biol. 2006 Sep;85(9-10):915-24. doi: 10.1016/j.ejcb.2006.05.002. Epub 2006 Jun 14. Eur J Cell Biol. 2006. PMID: 16781010 Review.
Cited by
-
Unified control of amoeboid pseudopod extension in multiple organisms by branched F-actin in the front and parallel F-actin/myosin in the cortex.PLoS One. 2020 Dec 9;15(12):e0243442. doi: 10.1371/journal.pone.0243442. eCollection 2020. PLoS One. 2020. PMID: 33296414 Free PMC article.
-
A model for a correlated random walk based on the ordered extension of pseudopodia.PLoS Comput Biol. 2010 Aug 12;6(8):e1000874. doi: 10.1371/journal.pcbi.1000874. PLoS Comput Biol. 2010. PMID: 20711349 Free PMC article.
-
Combining laser capture microdissection and proteomics reveals an active translation machinery controlling invadosome formation.Nat Commun. 2018 May 23;9(1):2031. doi: 10.1038/s41467-018-04461-9. Nat Commun. 2018. PMID: 29795195 Free PMC article.
-
Kindlin-1 Regulates Keratinocyte Electrotaxis.J Invest Dermatol. 2016 Nov;136(11):2229-2239. doi: 10.1016/j.jid.2016.05.129. Epub 2016 Jul 15. J Invest Dermatol. 2016. PMID: 27427485 Free PMC article.
-
Improved method for the quantification of motility in glia and other morphologically complex cells.Neural Plast. 2013;2013:853727. doi: 10.1155/2013/853727. Epub 2013 Nov 20. Neural Plast. 2013. PMID: 24349799 Free PMC article.
References
-
- Le Clainche C, Carlier MF. Regulation of actin assembly associated with protrusion and adhesion in cell migration. Physiol Rev. 2008;88:489–513. - PubMed
-
- Van Haastert PJM, Devreotes PN. Chemotaxis: signalling the way forward. Nat Rev Mol Cell Biol. 2004;5:626–634. - PubMed
-
- Pollard TD. Regulation of actin filament assembly by Arp2/3 complex and formins. Annu Rev Biophys Biomol Struct. 2007;36:451–477. - PubMed
-
- Arrieumerlou C, Meyer T. A local coupling model and compass parameter for eukaryotic chemotaxis. Dev Cell. 2005;8:215–227. - PubMed
-
- Costantino S, Kent CB, Godin AG, Kennedy TE, Wiseman PW, Fournier AE. Semi-automated quantification of filopodial dynamics. J Neurosci Methods. 2008;171:165–173. - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
