Discrete logic modelling as a means to link protein signalling networks with functional analysis of mammalian signal transduction
- PMID: 19953085
- PMCID: PMC2824489
- DOI: 10.1038/msb.2009.87
Discrete logic modelling as a means to link protein signalling networks with functional analysis of mammalian signal transduction
Abstract
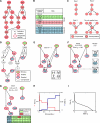
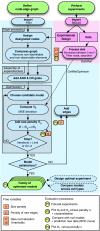
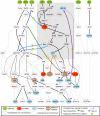
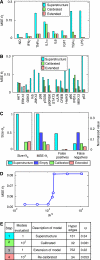
Large-scale protein signalling networks are useful for exploring complex biochemical pathways but do not reveal how pathways respond to specific stimuli. Such specificity is critical for understanding disease and designing drugs. Here we describe a computational approach--implemented in the free CNO software--for turning signalling networks into logical models and calibrating the models against experimental data. When a literature-derived network of 82 proteins covering the immediate-early responses of human cells to seven cytokines was modelled, we found that training against experimental data dramatically increased predictive power, despite the crudeness of Boolean approximations, while significantly reducing the number of interactions. Thus, many interactions in literature-derived networks do not appear to be functional in the liver cells from which we collected our data. At the same time, CNO identified several new interactions that improved the match of model to data. Although missing from the starting network, these interactions have literature support. Our approach, therefore, represents a means to generate predictive, cell-type-specific models of mammalian signalling from generic protein signalling networks.
Conflict of interest statement
The authors declare that they have no conflict of interest.
Figures



Similar articles
-
Creating and analyzing pathway and protein interaction compendia for modelling signal transduction networks.BMC Syst Biol. 2012 May 1;6:29. doi: 10.1186/1752-0509-6-29. BMC Syst Biol. 2012. PMID: 22548703 Free PMC article.
-
Training signaling pathway maps to biochemical data with constrained fuzzy logic: quantitative analysis of liver cell responses to inflammatory stimuli.PLoS Comput Biol. 2011 Mar;7(3):e1001099. doi: 10.1371/journal.pcbi.1001099. Epub 2011 Mar 3. PLoS Comput Biol. 2011. PMID: 21408212 Free PMC article.
-
Discrete Logic Modelling Optimization to Contextualize Prior Knowledge Networks Using PRUNET.PLoS One. 2015 Jun 9;10(6):e0127216. doi: 10.1371/journal.pone.0127216. eCollection 2015. PLoS One. 2015. PMID: 26058016 Free PMC article.
-
Unravelling the complexity of signalling networks in cancer: A review of the increasing role for computational modelling.Crit Rev Oncol Hematol. 2017 Sep;117:73-113. doi: 10.1016/j.critrevonc.2017.06.004. Epub 2017 Jun 23. Crit Rev Oncol Hematol. 2017. PMID: 28807238 Review.
-
A structured approach for the engineering of biochemical network models, illustrated for signalling pathways.Brief Bioinform. 2008 Sep;9(5):404-21. doi: 10.1093/bib/bbn026. Epub 2008 Jun 23. Brief Bioinform. 2008. PMID: 18573813 Review.
Cited by
-
TNF-insulin crosstalk at the transcription factor GATA6 is revealed by a model that links signaling and transcriptomic data tensors.Sci Signal. 2016 Jun 7;9(431):ra59. doi: 10.1126/scisignal.aad3373. Sci Signal. 2016. PMID: 27273097 Free PMC article.
-
Network dynamics-based subtyping of Alzheimer's disease with microglial genetic risk factors.Alzheimers Res Ther. 2024 Oct 16;16(1):229. doi: 10.1186/s13195-024-01583-9. Alzheimers Res Ther. 2024. PMID: 39415193 Free PMC article.
-
Comparative Network Reconstruction using mixed integer programming.Bioinformatics. 2018 Sep 1;34(17):i997-i1004. doi: 10.1093/bioinformatics/bty616. Bioinformatics. 2018. PMID: 30423075 Free PMC article.
-
Construction of the influenza A virus infection-induced cell-specific inflammatory regulatory network based on mutual information and optimization.BMC Syst Biol. 2013 Oct 20;7:105. doi: 10.1186/1752-0509-7-105. BMC Syst Biol. 2013. PMID: 24138989 Free PMC article.
-
Leveraging systems biology approaches in clinical pharmacology.Biopharm Drug Dispos. 2013 Dec;34(9):477-88. doi: 10.1002/bdd.1859. Epub 2013 Sep 17. Biopharm Drug Dispos. 2013. PMID: 23983165 Free PMC article. Review.
References
-
- Akaike H (1974) A new look at the statistical model identification. Automat Contr 19: 716–723
-
- Aldridge BB, Burke JM, Lauffenburger DA, Sorger PK (2006) Physicochemical modelling of cell signalling pathways. Nat Cell Biol 8: 1195–1203 - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

