Patient-specific wall stress analysis in cerebral aneurysms using inverse shell model

Abstract

Stress analyses of patient-specific vascular structures commonly assume that the reconstructed in vivo configuration is stress free although it is in a pre-deformed state. We submit that this assumption can be obviated using an inverse approach, thus increasing accuracy of stress estimates. In this paper, we introduce an inverse approach of stress analysis for cerebral aneurysms modeled as nonlinear thin shell structures, and demonstrate the method using a patient-specific aneurysm. A lesion surface derived from medical images, which corresponds to the deformed configuration under the arterial pressure, is taken as the input. The wall stress in the given deformed configuration, together with the unstressed initial configuration, are predicted by solving the equilibrium equations as opposed to traditional approach where the deformed geometry is assumed stress free. This inverse approach also possesses a unique advantage, that is, for some lesions it enables us to predict the wall stress without accurate knowledge of the wall elastic property. In this study, we also investigate the sensitivity of the wall stress to material parameters. It is found that the in-plane component of the wall stress is indeed insensitive to the material model.

FIGURE 1

Views of the stress-free configuration of a pressurized cerebral aneurysm predicted by the inverse shell approach. The predicted initial geometry (shaded) is visibly smaller than the in vivo shape (mesh). In the FE model, the nodes at the boundary edges are fixed.

FIGURE 2

Predicted principal stresses from the shell model with a Fung material. From left to right: the first principal membrane stress; the second principal membrane stress; the von Mises membrane stress. Unit of stress: N/mm².

FIGURE 3

Distribution of the shear stress norm. Unit: N/mm².

FIGURE 4

Distribution of the stress couple. Unit: N (torque per unit length).

FIGURE 5

Comparative stress distributions from the Fung models and the Mooney-Rivlin models. Unit of stress: N/mm². (a) Principal stresses in the baseline Fung model (c, d₁, d₂). From left to right: the first principal membrane stress; the second principal membrane stress; the von Mises membrane stress. (b) Principal stresses in the stiff Fung model (100c, d₁, d₂). (c) Principal stresses stress in the baseline Mooney-Rivlin model (μ₁, μ₂). (d) Principal stresses in the stiff Mooney-Rivlin model (100μ₁, 100μ₂).

FIGURE 6

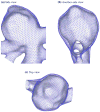
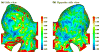
The percentage of the stress difference between the Mooney-Rivlin model (μ₁, μ₂) and the baseline Fung model (c, d₁, d₂) relative to a reference value 0.3 N/mm². From left to right: the percentage difference in the first principal membrane stress, the second principal membrane stress, and the von Mises membrane stress.