Impact of environmental inputs on reverse-engineering approach to network structures
- PMID: 19961587
- PMCID: PMC2799448
- DOI: 10.1186/1752-0509-3-113
Impact of environmental inputs on reverse-engineering approach to network structures
Abstract
Background: Uncovering complex network structures from a biological system is one of the main topic in system biology. The network structures can be inferred by the dynamical Bayesian network or Granger causality, but neither techniques have seriously taken into account the impact of environmental inputs.
Results: With considerations of natural rhythmic dynamics of biological data, we propose a system biology approach to reveal the impact of environmental inputs on network structures. We first represent the environmental inputs by a harmonic oscillator and combine them with Granger causality to identify environmental inputs and then uncover the causal network structures. We also generalize it to multiple harmonic oscillators to represent various exogenous influences. This system approach is extensively tested with toy models and successfully applied to a real biological network of microarray data of the flowering genes of the model plant Arabidopsis Thaliana. The aim is to identify those genes that are directly affected by the presence of the sunlight and uncover the interactive network structures associating with flowering metabolism.
Conclusion: We demonstrate that environmental inputs are crucial for correctly inferring network structures. Harmonic causal method is proved to be a powerful technique to detect environment inputs and uncover network structures, especially when the biological data exhibit periodic oscillations.
Figures
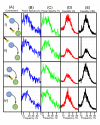
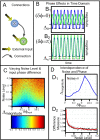
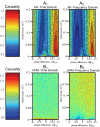
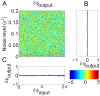


 or
or  depending upon whether the gene has an external input.
depending upon whether the gene has an external input.
Similar articles
-
Genome-wide dynamic network analysis reveals a critical transition state of flower development in Arabidopsis.BMC Plant Biol. 2019 Jan 7;19(1):11. doi: 10.1186/s12870-018-1589-6. BMC Plant Biol. 2019. PMID: 30616516 Free PMC article.
-
Reverse-engineering the Arabidopsis thaliana transcriptional network under changing environmental conditions.Genome Biol. 2009;10(9):R96. doi: 10.1186/gb-2009-10-9-r96. Epub 2009 Sep 15. Genome Biol. 2009. PMID: 19754933 Free PMC article.
-
Listen to genes: dealing with microarray data in the frequency domain.PLoS One. 2009;4(4):e5098. doi: 10.1371/journal.pone.0005098. Epub 2009 Apr 6. PLoS One. 2009. PMID: 22745650 Free PMC article.
-
Quantification of variation in expression networks.Methods Mol Biol. 2009;553:227-45. doi: 10.1007/978-1-60327-563-7_11. Methods Mol Biol. 2009. PMID: 19588108 Review.
-
Uncovering interactions in the frequency domain.PLoS Comput Biol. 2008 May 30;4(5):e1000087. doi: 10.1371/journal.pcbi.1000087. PLoS Comput Biol. 2008. PMID: 18516243 Free PMC article. Review.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

