Automated mass action model space generation and analysis methods for two-reactant combinatorially complex equilibriums: an analysis of ATP-induced ribonucleotide reductase R1 hexamerization data

Abstract

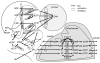
Background: Ribonucleotide reductase is the main control point of dNTP production. It has two subunits, R1, and R2 or p53R2. R1 has 5 possible catalytic site states (empty or filled with 1 of 4 NDPs), 5 possible s-site states (empty or filled with ATP, dATP, dTTP or dGTP), 3 possible a-site states (empty or filled with ATP or dATP), perhaps two possible h-site states (empty or filled with ATP), and all of this is folded into an R1 monomer-dimer-tetramer-hexamer equilibrium where R1 j-mers can be bound by variable numbers of R2 or p53R2 dimers. Trillions of RNR complexes are possible as a result. The problem is to determine which are needed in models to explain available data. This problem is intractable for 10 reactants, but it can be solved for 2 and is here for R1 and ATP.

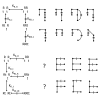
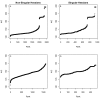
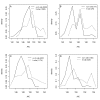
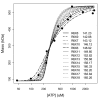
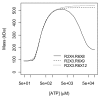
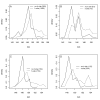
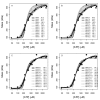
Results: Thousands of ATP-induced R1 hexamerization models with up to three (s, a and h) ATP binding sites per R1 subunit were automatically generated via hypotheses that complete dissociation constants are infinite and/or that binary dissociation constants are equal. To limit the model space size, it was assumed that s-sites are always filled in oligomers and never filled in monomers, and to interpret model terms it was assumed that a-sites fill before h-sites. The models were fitted to published dynamic light scattering data. As the lowest Akaike Information Criterion (AIC) of the 3-parameter models was greater than the lowest of the 2-parameter models, only models with up to 3 parameters were fitted. Models with sums of squared errors less than twice the minimum were then partitioned into two groups: those that contained no occupied h-site terms (508 models) and those that contained at least one (1580 models). Normalized AIC densities of these two groups of models differed significantly in favor of models that did not include an h-site term (Kolmogorov-Smirnov p < 1 x 10(-15)); consistent with this, 28 of the top 30 models (ranked by AICs) did not include an h-site term and 28/30 > 508/2088 with p < 2 x 10(-15). Finally, 99 of the 2088 models did not have any terms with ATP/R1 ratios >1.5, but of the top 30, there were 14 such models (14/30 > 99/2088 with p < 3 x 10(-16)), i.e. the existence of R1 hexamers with >3 a-sites occupied by ATP is also not supported by this dataset.

Conclusion: The analysis presented suggests that three a-sites may not be occupied by ATP in R1 hexamers under the conditions of the data analyzed. If a-sites fill before h-sites, this implies that the dataset analyzed can be explained without the existence of an h-site.

Figure 1

The dNTP supply system. Thick lines are fluxes, thin solid lines are activations, thin dashed lines are inhibitions. Key enzymes are described in the text. An RNR s-site mediated large positive feedback loop ATP → dCTP → dUMP → dTTP → dGTP → dATP terminates when dATP binds the R1 a-site to inhibit all 4 RNR reductions. Models of enzymes of this system will eventually be useful in anticancer drug dose time course optimizations [1].

Figure 2

ESI model graphs. The full spur graph at the top generates the seven models/graphs below it via hypotheses taken one at a time, two at a time, etc, that dissociation constants are infinite. The C-shaped grid graph is a data-fitting equivalent of the full spur graph. It generates the non-competitive inhibition model to its right where parallel edge binary K's are equal.

Figure 3

dTTP-induced R1 dimerization K equality models. The n-shaped graphs are equal to their corresponding E-shaped graphs below them. The rightmost three columns are very unlikely (see text). R = R1, t = dTTP and edges marked = or -- are alleged equal.

Figure 4

K equality RX model space. The graphs shown are the same for both a- and h-site models. The top two rows have independent threads and the bottom two rows have at least two threads that have equal binary K values indicated by =, --, or x. Bridge edges in the horizontal bars of each graph (i.e. the curtain rods) are spur edges from the hub, rather than binary K. Left to right, threads on curtain rods correspond to monomers, dimers, tetramers and hexamers.

Figure 5

AIC model densities versus AIC model rank. A) and C) show models that had non-singular Hessians (matrices of objective function second derivatives) at their optimums; B) and D) are models with singular (determinant = 0) Hessians, i.e. models that converged onto likelihood surfaces that were flat in one direction. C) and D) show 1613 and 475 models with SSEs < twice the minimum SSE.

Figure 6

Normalized AIC densities of models with SSEs less than twice the minimum. A) The models of Figs. 5C and 5D. There are 508 (1580) models without (with) an occupied h-site. B) The 1- and 2-parameter models of A). C) The 3-parameter models of A). D) The models in A) that have singular Hessians (i.e. the 475 models in Fig. 5D). In all cases a difference in h-site hypothesis densities is supported by a two-sample Kolmogorov-Smirnov test, P < 10^-15 (A, C, D) and P < 10^-5 (B).

Figure 7

Fits of the 1-parameter models. The legend in the plot indicates the model order ranked by AICs (values shown). The top 5 models are indicated by thicker lines. Beyond 5 or more a-sites occupied by ATP and with increasing numbers of h-sites occupied, the fits become worse and worse.

Figure 8

Top 3 fits to the data of Kashlan et al. [20]. A) Fits of the top 3 models. The second model uses its dimer term to capture a slight downturn in average mass at high [ATP] (see Fig. 9), consistent with its geometric mean binding constant being greater than that of the hexamer term in Table 1. Not shown in this plot is the point (0 μM, 90 kDa) which all models fit perfectly if M₁ = 90 is fixed (as it is here) rather than estimated. B) Residuals of the top model R6X8. The reduced variance and positive mean of the first 4 residuals may be due to bias arising from prior knowledge that the monomer is 90 kDa and thus too prior knowledge that the average mass must increase from 90 kDa. Non-weighted least squares gives less weight to these 4 points which, coincidentally, is advantageous given these suspicions. PlotDigitizer (Methods) was used to obtain the data from a pdf of the original paper, and as this step involves human intervention, it too may have introduced some bias and random error.

Figure 9

Model limits at large ligand concentrations. In the second model in Fig. 8 and Table 1 (solid line here) the dimer term R2X4 causes a below expectation peak (510 instead of 540) at high [ATP]. In the limit of very high [ATP], this model is dominated by the R2X4 term (average mass approaches 180 kDa) because this term partitions more X into a bound state with R than the hexamer R6X8, i.e. 4/2 = 2 > 8/6 = 1.3. These ratios are both 1.5 in the model R2X3.R6X9 (dashed line) which has a balanced population in this limit (with a limiting average mass of 523 kDa). These ratios are 1.5 and 2 in the model R2X3.R6X12 (dotted) which yields pure hexamers (average mass = 540 kDa) in the limit of infinite ATP.

Figure 10

Normalized model number densities of AICs of models with SSEs less than twice the minimum SSE and monotonic non-decreasing ratios of ATP per R1 as oligomer sizes increase. A) The complete set of such models. B) The 1- and 2-parameter models. C) The 3-parameter models. D) Models with singular Hessians. In all cases a difference in h-site hypothesis densities is supported by a two-sample Kolmogorov-Smirnov test, P < 10^-15 (A, C, D) and P < 2 × 10^-5 (B). Compare to Fig. 6.

Figure 11

The 13 single-edge spur models of Fig. 7(A) with p (B), M₁ (C) or both (D) estimated. The plots show that R⁶X⁹ should perhaps be trusted more than R⁶X⁸. AICs in the B-D legends suggest that R⁶X¹⁰ (which allows a 4^th filled a-site) is more likely than R⁶X⁷.

Figure 12

R1 hexamer model. R1 hexamer formation could result in the creation of two types of a-sites.

Figure 13

Fits of the top 3 models with [dTTP] and [GDP] at saturating levels. In response to reviewer Kashlan's comment, the top 3 models of the data in figure 5 of his paper are shown. All models yield m = 180 at [ATP] = 0; m = 181 was measured.

Figure 14

ccems code example. These codes generate Table 1 and the RX model space used in this paper.