A 2D mechanistic model of breast ductal carcinoma in situ (DCIS) morphology and progression
- PMID: 20006623
- PMCID: PMC2839055
- DOI: 10.1016/j.jtbi.2009.11.024
A 2D mechanistic model of breast ductal carcinoma in situ (DCIS) morphology and progression
Abstract
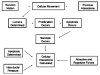
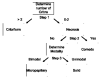
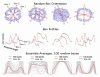
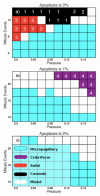
Ductal carcinoma in situ (DCIS) of the breast is a non-invasive tumor in which cells proliferate abnormally, but remain confined within a duct. Although four distinguishable DCIS morphologies are recognized, the mechanisms that generate these different morphological classes remain unclear, and consequently the prognostic strength of DCIS classification is not strong. To improve the understanding of the relation between morphology and time course, we have developed a 2D in silico particle model of the growth of DCIS within a single breast duct. This model considers mechanical effects such as cellular adhesion and intra-ductal pressure, and biological features including proliferation, apoptosis, necrosis, and cell polarity. Using this model, we find that different regions of parameter space generate distinct morphological subtypes of DCIS, so elucidating the relation between morphology and time course. Furthermore, we find that tumors with similar architectures may in fact be produced through different mechanisms, and we propose future work to further disentangle the mechanisms involved in DCIS progression.
(c) 2009 Elsevier Ltd. All rights reserved.
Figures



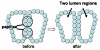



References
-
- Alarcón T, Byrne H, Maini P. A cellular automaton model for tumour growth in an inhomogeneous environment. Journal of Theoretical Biology. 2003;225:257–274. - PubMed
-
- Allred DC, Wu Y, Mao S, Nagtegaal ID, Lee S, Perou CM, Mohsin SK, O’Connell P, Tsimelzon A, Medina D. Ductal carcinoma in situ and the emergence of diversity during breast cancer evolution. Clin Cancer Res. 2008;14:370–8. - PubMed
-
- Ambrosi D, Mollica F. On the mechanics of a growing tumor. Int J Eng Sci. 2002;40:1297–1316.
-
- Anderson A, Weaver A, Cummings P, Quaranta V. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell. 2006;127:905–915. - PubMed
-
- Anderson AR, Quaranta V. Integrative mathematical oncology. Nat Rev Cancer. 2008;8:227–34. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

