Temporal self-organization of the cyclin/Cdk network driving the mammalian cell cycle
- PMID: 20007375
- PMCID: PMC2799800
- DOI: 10.1073/pnas.0903827106
Temporal self-organization of the cyclin/Cdk network driving the mammalian cell cycle
Abstract
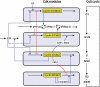
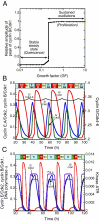
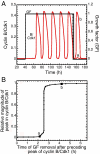
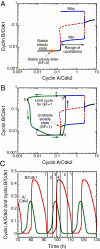
We propose an integrated computational model for the network of cyclin-dependent kinases (Cdks) that controls the dynamics of the mammalian cell cycle. The model contains four Cdk modules regulated by reversible phosphorylation, Cdk inhibitors, and protein synthesis or degradation. Growth factors (GFs) trigger the transition from a quiescent, stable steady state to self-sustained oscillations in the Cdk network. These oscillations correspond to the repetitive, transient activation of cyclin D/Cdk4-6 in G(1), cyclin E/Cdk2 at the G(1)/S transition, cyclin A/Cdk2 in S and at the S/G(2) transition, and cyclin B/Cdk1 at the G(2)/M transition. The model accounts for the following major properties of the mammalian cell cycle: (i) repetitive cell cycling in the presence of suprathreshold amounts of GF; (ii) control of cell-cycle progression by the balance between antagonistic effects of the tumor suppressor retinoblastoma protein (pRB) and the transcription factor E2F; and (iii) existence of a restriction point in G(1), beyond which completion of the cell cycle becomes independent of GF. The model also accounts for endoreplication. Incorporating the DNA replication checkpoint mediated by kinases ATR and Chk1 slows down the dynamics of the cell cycle without altering its oscillatory nature and leads to better separation of the S and M phases. The model for the mammalian cell cycle shows how the regulatory structure of the Cdk network results in its temporal self-organization, leading to the repetitive, sequential activation of the four Cdk modules that brings about the orderly progression along cell-cycle phases.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
References
-
- Blagosklonny MV, Pardee AB. The restriction point of the cell cycle. Cell Cycle. 2002;1:103–110. - PubMed
-
- Morgan DO. The Cell Cycle: Principles of Control. Oxford: Oxford Univ Press; 2006.
-
- Nurse P. Cyclin-dependent kinases and cell cycle control. ChemBioChem. 2002;3:596–603. - PubMed
-
- Malumbres M, Barbacid M. Mammalian cyclin-dependent kinases. Trends Biochem Sci. 2005;30:630–641. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
Miscellaneous

