Evolutionary dynamics in structured populations
- PMID: 20008382
- PMCID: PMC2842709
- DOI: 10.1098/rstb.2009.0215
Evolutionary dynamics in structured populations
Abstract
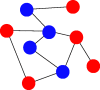
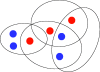
Evolutionary dynamics shape the living world around us. At the centre of every evolutionary process is a population of reproducing individuals. The structure of that population affects evolutionary dynamics. The individuals can be molecules, cells, viruses, multicellular organisms or humans. Whenever the fitness of individuals depends on the relative abundance of phenotypes in the population, we are in the realm of evolutionary game theory. Evolutionary game theory is a general approach that can describe the competition of species in an ecosystem, the interaction between hosts and parasites, between viruses and cells, and also the spread of ideas and behaviours in the human population. In this perspective, we review the recent advances in evolutionary game dynamics with a particular emphasis on stochastic approaches in finite sized and structured populations. We give simple, fundamental laws that determine how natural selection chooses between competing strategies. We study the well-mixed population, evolutionary graph theory, games in phenotype space and evolutionary set theory. We apply these results to the evolution of cooperation. The mechanism that leads to the evolution of cooperation in these settings could be called 'spatial selection': cooperators prevail against defectors by clustering in physical or other spaces.
Figures

References
-
- Antal T., Nowak M. A., Traulsen A.2009aStrategy abundance in 2 × 2 games for arbitrary mutation rates. J. Theor. Biol. 257, 340–344 (doi:10.1016/j.jtbi.2008.11.023) - DOI - PMC - PubMed
-
- Antal T., Traulsen A., Ohtsuki H., Tarnita C. E., Nowak M. A.2009bMutation–selection equilibrium in games with multiple strategies. J. Theor. Biol. 258, 614–622 (doi:10.1016/j.jtbi.2009.02.010) - DOI - PMC - PubMed
-
- Antal T., Ohtsuki H., Wakeley J., Taylor P. D., Nowak M. A.2009cEvolutionary game dynamics in phenotype space. Proc. Natl Acad. Sci. USA 106, 8597–8600 (doi:10.1073/pnas.0902528106) - DOI - PMC - PubMed
-
- Axelrod R., Hamilton W. D.1981The evolution of cooperation. Science 211, 1390–1396 (doi:10.1126/science.7466396) - DOI - PubMed
-
- Binmore K.2007Playing for real: a text on game theory Oxford, UK: Oxford University Press
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
