Generating spatiotemporal joint torque patterns from dynamical synchronization of distributed pattern generators

Abstract

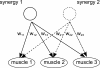
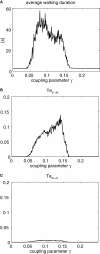
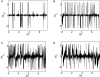
Pattern generators found in the spinal cord are no more seen as simple rhythmic oscillators for motion control. Indeed, they achieve flexible and dynamical coordination in interaction with the body and the environment dynamics giving to rise motor synergies. Discovering the mechanisms underlying the control of motor synergies constitutes an important research question not only for neuroscience but also for robotics: the motors coordination of high dimensional robotic systems is still a drawback and new control methods based on biological solutions may reduce their overall complexity. We propose to model the flexible combination of motor synergies in embodied systems via partial phase synchronization of distributed chaotic systems; for specific coupling strength, chaotic systems are able to phase synchronize their dynamics to the resonant frequencies of one external force. We take advantage of this property to explore and exploit the intrinsic dynamics of one specified embodied system. In two experiments with bipedal walkers, we show how motor synergies emerge when the controllers phase synchronize to the body's dynamics, entraining it to its intrinsic behavioral patterns. This stage is characterized by directed information flow from the sensors to the motors exhibiting the optimal situation when the body dynamics drive the controllers (mutual entrainment). Based on our results, we discuss the relevance of our findings for modeling the modular control of distributed pattern generators exhibited in the spinal cord, and for exploring the motor synergies in robots.

Keywords: causal information flow; motor synergies; phase synchronization; sensorimotor coordination.

Figure 1

Concept of motor synergies. One motor synergy constitutes particular grouping of muscles for certain weights configurations (Bizzi and Clarac, 1999). In the same time, one muscle can be activated by several synergies (Ting, 2007); this demonstrates how modular and flexible the motor system is.

Figure 2

Phase synchronization. For specific coupling values γ, a chaotic system is able to match and combine the natural resonance frequencies of two or more forces.

Figure 3

Joint mechanism of phase synchronization and feedback resonance between an active system and a dissipative system. Depending on the values of the coupling parameter {γ}, the chaotic oscillator synchronizes or not to the phase of the dissipative system.The occurrence of this stage produces a resonance regime in the device. In our framework, we conceive motor synergies as the mutual entrainment between the internal controller and the dissipative system.

Figure 4

Control architecture for the compass biped walker coupled to one chaotic system. We hypothetize that for specific coupling values γ₁ and γ₂, we will have the chaotic system matching the phase of the walker dynamics.

Figure 5

The pace of the compass walker is described by the amplitude of its hip angle A(t) plotted in (A) and the controller dynamics plotted in plain lines in (B). Its stride is not fixed but dynamic as the amplitude of the hip angle varies from small ranges to higher ones. The chaotic map's fast dynamics match and entrain its envelope to the biped's dynamics (dashed line plotted below). The coupling between the two systems is set symmetrically with γ₁ = γ₂ = 0.1, and μ = 1.95.

Figure 6

Phase plot of the biped hip angle's amplitude variation during locomotion (A) and its evolution over time (B); the time delay is set to 50 ms with a sampling time of 5 ms. The hip torques trajectory follows the intrinsic attractor in which the biped belongs. Its dynamics converge sometimes to it and sometimes slightly diverge from it.

Figure 7

Sensorimotor information flow for γ₁ = γ₂ = γ ∈ [0; 0.25] over 50 trials for each values. (A) Plot of the average walking duration stability (in seconds) dependent to the coupling strength γ. Transfer entropy measure of resp. Te_S→M in (B) corresponding to the causal influence of the body on the controller dynamics, and Te_M→S in (C) corresponding to the causal influence induced by the controller on the body dynamics. The stable walking area γ ∈ [0.05, 0.015] corresponds to inverted and asymmetric information flow from the body dynamics over the controller for which Te_S→M >> Te_M→S: the body controls the controller (!). Phase synchronization permits the controller to fully exploit the body dynamics in order to control it in return.

Figure 8

Control scheme of the kneed biped. Each joint is linearly coupled to a chaotic unit receiving in return its joint angle. The sensory inputs are pondered by the coupling parameter ε₁, and the motor outputs are weighted by ε₂. Hence, the pair {ε₁, ε₂} controls the whole biped's dynamics. The limbs coordination arise when the isolated chaotic units globally phase synchronize to each other through the body.

Figure 9

Control scheme of the kneed biped from Figure 8. The variables {ε₁, ε₂} linearly couple the chaotic oscillators to their respective limbs (left). However, due to their embodiment, the isolated controllers receive dynamically the phase information from the different body parts: the situation is comparable to the schema in the right side where the pair {ε₁, ε₂} controls the global level of synchronization. In this parameter space, particular values will correspond to characteristic limbs coordinations (i.e., its motor synergies).

Figure 10

Walking duration performance map for the kneed biped for the control parameters pair {G, ε₂} ∈ [0; 1] × [0; 20] in (A) and {ε₁, ε₂} ∈ [0; 1] × [0; 1] in (B). They reveal hidden information structure and correlations for particular coupling strengths. These relations correspond to the stable coordinations occurring between the internal controllers and the biped dynamics, its intrinsic behavioral patterns.

Figure 11

Motion sequence of the kneed biped walker for the parameters ε₁ = 0. 10, ε₂ = 0.10, output Gain G = 10. The body and the controllers mutually entrain themselves with each other in an emergent manner. The body dynamics feeded back to the controllers contribute to regulate its own motion.

Figure 12

Time series of the sensors and motor dynamics for the parameters {ε₁, ε₂, G} ∈ [0; 1] × [0; 1] × [10]. (A) time series of the joint angles of the hip Δβ, of the knees γ_{L,R}, of the torso alpha, and their respective torque command activation in (B) resp. F_Δβ, F_γ{L,R}, and F_α. Regular sensorimotor patterns are discovered and stabilized dynamically in the whole system, i.e., partial and dynamic phase synchronization (see the dashed and plain lines in (A)) – till one perturbation destroys the coordination.

Figure 13

Phase difference Δφ evolution between the biped sensors and motor dynamics during locomotion. The coordination in each joint is dynamic with lot of variance, however stable since centered in 0.

Figure 14

Phase plots and causality measure of the sensorimotor information flow in all the joints during walking; resp. left and right column. In the right, the causal flows from the body dynamics X to its controller F_X, $T{e}_{X\text{→}{F}_X},$ are drawn in plain lines. The causal flows from the controller F_X to its sensory variable X, $T{e}_{F_X\text{→}X},$ are drawn in dashed lines. During walking, the body and the controllers flexibly entrain themselves dynamically. This coordination depends bothly on the current posture of the body and on the ongoing internal dynamics. However, the causal flows between the two systems reveals that the body drives most of the time the internal dynamics $(T{e}_{X\text{→}{F}_X}\text{>}T{e}_{F_X\text{→}X})$ which means that the controllers exploit efficiently the body passive dynamics. Nevertheless, for short periods, the causal flow in the embodied system is inverted (when we have $T{e}_{X\text{→}{F}_X}\text{≤}T{e}_{F_X\text{→}X}$) exhibiting the situation when the controllers actively drive the biped.

Figure 15

Model of the compass-gait biped.

Figure 16

Model of the biped walker with knees.