Numerical modeling of long bone adaptation due to mechanical loading: correlation with experiments

Abstract

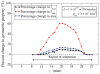
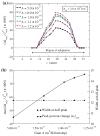
The process of external bone adaptation in cortical bone is modeled mathematically using finite element (FE) stress analysis coupled with an evolution model, in which adaptation response is triggered by mechanical stimulus represented by strain energy density. The model is applied to experiments in which a rat ulna is subjected to cyclic loading, and the results demonstrate the ability of the model to predict the bone adaptation response. The FE mesh is generated from micro-computed tomography (microCT) images of the rat ulna, and the stress analysis is carried out using boundary and loading conditions on the rat ulna obtained from the experiments [Robling, A. G., F. M. Hinant, D. B. Burr, and C. H. Turner. J. Bone Miner. Res. 17:1545-1554, 2002]. The external adaptation process is implemented in the model by moving the surface nodes of the FE mesh based on an evolution law characterized by two parameters: one that captures the rate of the adaptation process (referred to as gain); and the other characterizing the threshold value of the mechanical stimulus required for adaptation (referred to as threshold-sensitivity). A parametric study is carried out to evaluate the effect of these two parameters on the adaptation response. We show, following comparison of results from the simulations to the experimental observations of Robling et al. (J. Bone Miner. Res. 17:1545-1554, 2002), that splitting the loading cycles into different number of bouts affects the threshold-sensitivity but not the rate of adaptation. We also show that the threshold-sensitivity parameter can quantify the mechanosensitivity of the osteocytes.

FIG. 1

The finite element model of the rat ulna constructed from micro computed tomography images. The mesh contains 62,789 nodes and 37,000 elements. A compressive load of 9 N is applied to the right end (proximal end) and a node at the left end (the distal end) is fixed.

FIG. 2

Demonstration of the smoothing procedure on a circular cylinder. (a) w =1 (local data only) produces a jagged surface. (b) w = 0 (local information about the stimulus is lost) leading to rippled surfaces. (c) w = 0.5 produces a smooth surface.

FIG. 3

Flowchart of the external adaptation algorithm.

FIG. 4

Strain energy density contour plots of (a) original ulna and (b) adapted ulna. Grey regions denote elements with strain energy density greater than 1.1 × 10⁵ J/m³. We can clearly see that the strain energy density is reduced in the adapted ulna, due to the added bone.

FIG. 5

Comparison of the overlay plots of the rat ulna midshaft from simulation (left) and experiments of Robling et al. (right). The dotted line on the left corresponds to the original bone and the solid line corresponds to the grown bone cross section in the simulation. The red line on the right corresponds to the original bone and the outer dark green solid line corresponds to the grown bone cross section in the experiments. The experiments lasted 16 weeks.

FIG. 6

Plot showing the percent change in the geometric properties of cross-sections (I_max, I_min and area) between the original and grown ulna after 20 timesteps for the baseline values of parameters A and φ_ref.

FIG. 7

Comparison of the percent change in the minimum principal moments of inertia I_min between the original and adapted ulna from external bone adaptation simulations and experiments of Robling et al. The error bars shown for the experimental data correspond to one standard deviation. ΔI_min is the change in the minimum moment of inertia between the original and adapted ulna and $I_{min}^0$ is the minimum moment of inertia of the original ulna.

FIG. 8

Plots showing the (a) effect of timesteps on the percent change in I_min and (b) variation of peak of percent increase in I_min with number of timesteps on the external bone adaptation simulation. ΔI_min is the change in the minimum moment of inertia between the original and adapted ulna and $I_{min}^0$ is the minimum moment of inertia of the original ulna.

FIG. 9

Plots showing the (a) effect of gain A on the percent change in I_min and (b) variation of peak value of percent increase in I_min and width at half peak with respect to A on the external bone adaptation simulation. ΔI_min is the change in the minimum moment of inertia between the original and adapted ulna and $I_{min}^0$ is the minimum moment of inertia of the original ulna.

FIG. 10

Plots showing the (a) effect of sensitivity φ_ref on the percent change in I_min, and (b) variation of peak value of percent increase in I_min and width at half peak with respect to sensitivity on the external bone adaptation simulation. ΔI_min is the change in the minimum moment of inertia between the original and adapted ulna and $I_{min}^0$ is the minimum moment of inertia of the original ulna.