A computationally efficient formal optimization of regional myocardial contractility in a sheep with left ventricular aneurysm
- PMID: 20016753
- PMCID: PMC2793686
- DOI: 10.1115/1.3148464
A computationally efficient formal optimization of regional myocardial contractility in a sheep with left ventricular aneurysm
Abstract
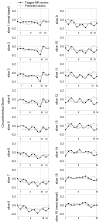
A non-invasive method for estimating regional myocardial contractility in vivo would be of great value in the design and evaluation of new surgical and medical strategies to treat and/or prevent infarction-induced heart failure. As a first step towards developing such a method, an explicit finite element (FE) model-based formal optimization of regional myocardial contractility in a sheep with left ventricular (LV) aneurysm was performed using tagged magnetic resonance (MR) images and cardiac catheterization pressures. From the tagged MR images, 3-dimensional (3D) myocardial strains, LV volumes and geometry for the animal-specific 3D FE model of the LV were calculated, while the LV pressures provided physiological loading conditions. Active material parameters (T(max_B) and T(max_R)) in the non-infarcted myocardium adjacent to the aneurysm (borderzone) and in myocardium remote from the aneurysm were estimated by minimizing the errors between FE model-predicted and measured systolic strains and LV volumes using the successive response surface method for optimization. The significant depression in optimized T(max_B) relative to T(max_R) was confirmed by direct ex vivo force measurements from skinned fiber preparations. The optimized values of T(max_B) and T(max_R) were not overly sensitive to the passive material parameters specified. The computation time of less than 5 hours associated with our proposed method for estimating regional myocardial contractility in vivo makes it a potentially very useful clinical tool.
Keywords: cardiac mechanics; finite element modeling; numerical optimization; tagged magnetic resonance imaging.
Figures






Similar articles
-
Regional left ventricular myocardial contractility and stress in a finite element model of posterobasal myocardial infarction.J Biomech Eng. 2011 Apr;133(4):044501. doi: 10.1115/1.4003438. J Biomech Eng. 2011. PMID: 21428685 Free PMC article.
-
A novel method for quantifying in-vivo regional left ventricular myocardial contractility in the border zone of a myocardial infarction.J Biomech Eng. 2011 Sep;133(9):094506. doi: 10.1115/1.4004995. J Biomech Eng. 2011. PMID: 22010752 Free PMC article.
-
A Novel Method for Quantifying Smooth Regional Variations in Myocardial Contractility Within an Infarcted Human Left Ventricle Based on Delay-Enhanced Magnetic Resonance Imaging.J Biomech Eng. 2015 Aug;137(8):081009. doi: 10.1115/1.4030667. Epub 2015 Jun 16. J Biomech Eng. 2015. PMID: 25994000 Free PMC article.
-
Clinical aspects of left ventricular diastolic function assessed by Doppler echocardiography following acute myocardial infarction.Dan Med Bull. 2001 Nov;48(4):199-210. Dan Med Bull. 2001. PMID: 11767125 Review.
-
Defining the relationship between akinesia and dyskinesia and the cause of left ventricular failure after anterior infarction and reversal of remodeling to restoration.J Thorac Cardiovasc Surg. 1998 Jul;116(1):47-9. doi: 10.1016/s0022-5223(98)70241-7. J Thorac Cardiovasc Surg. 1998. PMID: 9671896 Review. No abstract available.
Cited by
-
The benefit of enhanced contractility in the infarct borderzone: a virtual experiment.Front Physiol. 2012 Apr 9;3:86. doi: 10.3389/fphys.2012.00086. eCollection 2012. Front Physiol. 2012. PMID: 22509168 Free PMC article.
-
Biomechanics of infarcted left ventricle: a review of modelling.Biomed Eng Lett. 2020 Jun 10;10(3):387-417. doi: 10.1007/s13534-020-00159-4. eCollection 2020 Aug. Biomed Eng Lett. 2020. PMID: 32864174 Free PMC article. Review.
-
Bioinjection treatment: effects of post-injection residual stress on left ventricular wall stress.J Biomech. 2014 Sep 22;47(12):3115-9. doi: 10.1016/j.jbiomech.2014.06.026. Epub 2014 Jun 25. J Biomech. 2014. PMID: 25065728 Free PMC article.
-
Regional assessment of in vivo myocardial stiffness using 3D magnetic resonance elastography in a porcine model of myocardial infarction.Magn Reson Med. 2018 Jan;79(1):361-369. doi: 10.1002/mrm.26695. Epub 2017 Apr 5. Magn Reson Med. 2018. PMID: 28382658 Free PMC article.
-
First evidence of depressed contractility in the border zone of a human myocardial infarction.Ann Thorac Surg. 2012 Apr;93(4):1188-93. doi: 10.1016/j.athoracsur.2011.12.066. Epub 2012 Feb 9. Ann Thorac Surg. 2012. PMID: 22326127 Free PMC article.
References
-
- Guccione JM, Walker JC, Beitler JR, Moonly SM, Zhang P, Guttman MA, Ozturk C, McVeigh ER, Wallace AW, Saloner DA, Ratcliffe MB. The effect of anteroapical aneurysm plication on end-systolic three-dimensional strain in the sheep: a magnetic resonance imaging tagging study. J Thorac Cardiovasc Surg. 2006;131(3):579–586 e3. - PMC - PubMed
-
- Walker JC, Guccione JM, Jiang Y, Zhang P, Wallace AW, Hsu EW, Ratcliffe MB. Helical myofiber orientation after myocardial infarction and left ventricular surgical restoration in sheep. J Thorac Cardiovasc Surg. 2005;129(2):382–90. - PubMed
-
- Costa KD, Hunter PJ, Wayne JS, Waldman LK, Guccione JM, McCulloch AD. A three-dimensional finite element method for large elastic deformations of ventricular myocardium: II--Prolate spheroidal coordinates. J Biomech Eng. 1996;118(4):464–72. - PubMed
-
- Walker JC, Ratcliffe MB, Zhang P, Wallace AW, Fata B, Hsu EW, Saloner D, Guccione JM. MRI-based finite-element analysis of left ventricular aneurysm. Am J Physiol Heart Circ Physiol. 2005;289(2):H692–700. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

