Influenza--insights from mathematical modelling

Abstract

Background: When the first cases of a new infectious disease appear, questions arise about the further course of the epidemic and about the appropriate interventions to be taken to protect individuals and the public as a whole. Mathematical models can help answer these questions. In this article, the authors describe basic concepts in the mathematical modelling of infectious diseases, illustrate their use with a simple example, and present the results of influenza models.

Method: Description of the mathematical modelling of infectious diseases and selective review of the literature.

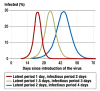
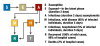
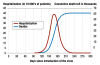
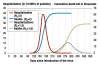
Results: The two fundamental concepts of mathematical modelling of infectious diseases-the basic reproduction number and the generation time-allow a better understanding of the course of an epidemic. Modelling studies based on past influenza epidemics suggest that the rise of the epidemic curve can be slowed at the beginning of the epidemic by isolating ill persons and giving prophylactic medications to their contacts. Later on in the course of the epidemic, restricting the number of contacts (e.g., by closing schools) may mitigate the epidemic but will only have a limited effect on the total number of persons who contract the disease.

Conclusion: Mathematical modelling is a valuable tool for understanding the dynamics of an epidemic and for planning and evaluating interventions.

Keywords: disease course; epidemic; infection control; influenza; prevention.

Figure 1

a) The typical course of an influenza epidemic in a fully susceptible population. The curves show the proportion of the population which is severely ill or convalescing on varying days—based on the assumption that only a third of all infected individuals would become severely ill (source: www.influsim.de). The basic reproduction numbers for the curves are (from left to right): 3.0 (Grey), 2.0 (Red), 1.5 (Green), 1.3 (Blue) and 1.2 (Yellow). b) The proportion of the population who would be infected during the course of an epidemic dependant on the various basic reproduction numbers

Figure 2

The number of infected individuals in the course of an epidemic. The basic rate of reproduction R0 is set at 2.0 for all of the curves, the duration of the latent and infectious periods varies. Red curve: 1 day latent, 2 days infectious. Green Curve: 1.5 days latent, 3 days infectious. Blue Curve: 2 days latent, 4 days infectious.

Figure 3

Expanded SEIR (susceptible-exposed-infectious-removed) Model (the infectious group in this model is composed of groups A, M and H)

Figure 4

Example of the possible course of an influenza epidemic (using the model from Figure 3)

Figure 5

Hospitalization and deaths during the course of the example epidemic

Figure 6

Effects of a reduction in R0 on hospitalization rates and deaths