Evaluation of different tests based on observations for external model evaluation of population analyses

Abstract

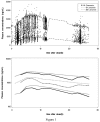
To evaluate by simulation the statistical properties of normalized prediction distribution errors (NPDE), prediction discrepancies (pd), standardized prediction errors (SPE), numerical predictive check (NPC) and decorrelated NPC (NPC(dec)) for the external evaluation of a population pharmacokinetic analysis, and to illustrate the use of NPDE for the evaluation of covariate models. We assume that a model M(B) has been built using a building dataset B, and that a separate validation dataset, V is available. Our null hypothesis H(0) is that the data in V can be described by M(B). We use several methods to test this hypothesis: NPDE, pd, SPE, NPC and NPC(dec). First, we evaluated by simulation the type I error under H(0) of different tests applied to the four methods. We also propose and evaluate a single global test combining normality, mean and variance tests applied to NPDE, pd and SPE. We perform tests on NPC and NPC(dec), after a decorrelation. M(B) was a one compartment model with first order absorption (without covariate), previously developed from two phase II and one phase III studies of the antidiabetic drug, gliclazide. We simulated 500 external datasets according to the design of a phase III study. Second, we investigated the application of NPDE to covariate models. We propose two approaches: the first approach uses correlation tests or mean comparisons to test the relationship between NPDE and covariates; the second evaluates NPDE split by category for discrete covariates or quantiles for continuous covariates. We generated several validation datasets under H(0) and under alternative assumptions with a model without covariate, with one continuous covariate (weight), or one categorical covariate (sex). We calculated the powers of the different tests using simulations, where the covariates of the phase III study were used. The simulations under H(0) show a high type I error for the different tests applied to SPE and an increased type I error for pd. The different tests present a type I error close to 5% for the global test appied to NPDE. We find a type I error higher than 5% for the test applied to classical NPC but this test becomes close to 5% for NPC(dec). For covariate models, when model and validation dataset are consistent, type I error of the tests are close to 5% for both effects. When validation datasets and models are not consistent, the tests detect the correlation between NPDE and the covariate. We recommend to use NPDE over SPE for external model evaluation, since they do not depend on an approximation of the model and have good statistical properties. NPDE represent a better approach than NPC, since in order to perform tests on NPC, a decorrelation step must be applied before. NPDE, in this illustration, is also a good tool to evaluate model with or without covariates.

Figure 1

Gliclazide plasma concentration normalized for a dose of 30 mg versus time. On the top plot, the black dots represent the observations and the dashed lines the 5^th and 95^th percentiles of 1000 simulations. On the bottom plot, the black lines represent the 10^th, 50^th and 90^th percentiles of 1000 simulations. The gray lines represent the 10^th, 50^th and 90^th percentiles of the observations.

Figure 2

Illustration of how to compute prediction discrepancies (pd), also used to compute NPDE. In the left top plot, dots represent observed plasma concentrations versus time and the dashed lines represent the 90% predicted interval, obtained as the 5^th and 95^th percentiles of simulations. In the left bottom plot; the predicted distribution of an observed concentration (Y_ij) is represented in order to define the pd. In the right bottom plot, the distribution of pd is represented.

Figure 3

Box-plots of the Normalized Prediction Distribution Errors (NPDE) versus a continuous covariate (weight) categorized into 3 classes. V₀ denotes a dataset simulated under H₀ with the model M₀ and V_WT a dataset simulated assuming an effect of weight on V/F (model M_WT). In the left hand plot, NPDE were computed for V₀ with simulations under M₀; in the middle plot, NPDE were computed for V_WT with simulations under M₀; in the right hand plot, NPDE were computed for V₀ with simulations under M_WT.

Figure 4

Box-plots of the Normalized Prediction Distribution Errors (NPDE) versus a categorical covariate (sex) with M for male and F for female. V₀ denotes a dataset simulated under H₀ with the model M₀ and V_SEX a dataset simulated assuming an effect of SEX on CL/F (model M_SEX). In the left hand plot, NPDE were computed for V₀ with simulations under M₀; in the middle plot, NPDE were computed for V_SEX with simulations under M₀; in the right hand plot, NPDE were computed for V₀ with simulations under M_SEX.

Figure 5

Cumulative density function (cdf) plots of the Normalized Prediction Distribution Errors (NPDE) split by sex. In the top plots NPDE were computed for V₀ with simulations under M₀; in the middle plots, NPDE were computed for V_SEX with simulations under M₀; in bottom plots, NPDE were computed for V₀ with simulations under M_SEX.