Mode-locked spike trains in responses of ventral cochlear nucleus chopper and onset neurons to periodic stimuli
- PMID: 20042702
- PMCID: PMC2887620
- DOI: 10.1152/jn.00070.2009
Mode-locked spike trains in responses of ventral cochlear nucleus chopper and onset neurons to periodic stimuli
Abstract
We report evidence of mode-locking to the envelope of a periodic stimulus in chopper units of the ventral cochlear nucleus (VCN). Mode-locking is a generalized description of how responses in periodically forced nonlinear systems can be closely linked to the input envelope, while showing temporal patterns of higher order than seen during pure phase-locking. Re-analyzing a previously unpublished dataset in response to amplitude modulated tones, we find that of 55% of cells (6/11) demonstrated stochastic mode-locking in response to sinusoidally amplitude modulated (SAM) pure tones at 50% modulation depth. At 100% modulation depth SAM, most units (3/4) showed mode-locking. We use interspike interval (ISI) scattergrams to unravel the temporal structure present in chopper mode-locked responses. These responses compared well to a leaky integrate-and-fire model (LIF) model of chopper units. Thus the timing of spikes in chopper unit responses to periodic stimuli can be understood in terms of the complex dynamics of periodically forced nonlinear systems. A larger set of onset (33) and chopper units (24) of the VCN also shows mode-locked responses to steady-state vowels and cosine-phase harmonic complexes. However, while 80% of chopper responses to complex stimuli meet our criterion for the presence of mode-locking, only 40% of onset cells show similar complex-modes of spike patterns. We found a correlation between a unit's regularity and its tendency to display mode-locked spike trains as well as a correlation in the number of spikes per cycle and the presence of complex-modes of spike patterns. These spiking patterns are sensitive to the envelope as well as the fundamental frequency of complex sounds, suggesting that complex cell dynamics may play a role in encoding periodic stimuli and envelopes in the VCN.
Figures

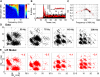




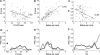
References
-
- Aihara K, Matsumoto G, Ikegaya Y. Periodic and non-periodic responses of a periodically forced Hodgkin-Huxley oscillator. J Theo Biol 109: 249–269, 1984 - PubMed
-
- Arle JE, Kim DO. Neural modeling of intrinsic and spike-discharge properties of cochlear nucleus neurons. Biol Cybern 64: 273–283, 1991 - PubMed
-
- Bal R, Oertel D. Potassium currents in octopus cells of the mammalian cochlear nucleus. J Neurophysiol 86: 2299–2311, 2001 - PubMed
-
- Banks MI, Sachs MB. Regularity analysis in a compartmental model of chopper units in the anteroventral cochlear nucleus. J Neurophysiol 65: 606–629, 1991 - PubMed
-
- Blackburn CC, Sachs MB. Classification of unit types in the anteroventral cochlear nucleus: PST histograms and regularity analysis. J Neurophysiol 62: 1303–1329, 1989 - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

