Perceiving parts and shapes from concave surfaces

Abstract

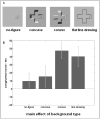
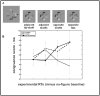
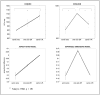
"A hole is nothing at all, but it can break your neck." In a similar fashion to the danger illustrated by this folk paradox, concave regions pose difficulties to theories of visual shape perception. We can readily identify their shapes, but according to principles of how observers determine part boundaries, concavities in a planar surface should have very different figural shapes from the ones that we perceive. In three experiments, we tested the hypothesis that observers perceive local image features differently in simulated 3-D concave and convex regions but use them to arrive at similar shape percepts. Stimuli were shape-from-shading images containing regions that appeared either concave or convex in depth, depending on their orientation in the picture plane. The results show that concavities did not benefit from the same global object-based attention or holistic shape encoding as convexities and that the participants relied on separable spatial dimensions to judge figural shape in concavities. Concavities may exploit a secondary process for shape perception that allows regions composed of perceptually independent features to ultimately be perceived as gestalts.

Figure 1

The type of hole that is the focus of this study. Left: a concavity bounded by a flat plane, with a closed bounding contour. Middle: the concavity shown as an indentation in a planar sheet. Right: the concavity shown rotated 180° in depth so that it appears as a convex bulge with the same 2D bounding contour.

Figure 2

Top: Minima of curvature marked on a 2D cross shape. These minima of curvature correspond to minima that cut through the sides of a 3D convexity, but not to those of a 3D concavity, which are complementary. Middle: These minima of curvature marked on equivalent convex and concave 3D versions of the cross shape. There are twice as many minima cutting through the sides in the concave version. Bottom: Part structures (indicated by different image textures) based on the convex and concave minima and on the “shortcut rule” of Singh et al. (1999). It is unclear precisely how the concave image’s part boundaries radiate out past the cusp of the concavity. However, since the cusp itself is a maximum of curvature, the facets oriented in depth which form the sides of the concavity belong with regions of the surrounding plane, rather than with the surface forming the bottom of the hole.

Figure 3

A: schematic illustration of stimulus backgrounds used in Experiment 1. Hatched and dotted regions represent differently colored surface patches for clarity. All examples show the adjacent tip-shaft surface pair for clarity of comparison. B: main effect of stimulus background on congruence scores.

Figure 4

A: Schematic illustration of surface pair combinations used. Only surface pigmentation was altered to highlight surfaces in the actual stimuli; hatching is drawn for clarity. B: Congruence scores based on median RTs. Scores from the no-figure baseline condition have been subtracted out. Error bars represent standard error of the mean.

Figure 5

Examples of the three 3D-rendered stimulus types used in Experiment 2. The convex and ambiguous stimuli were created by rotating the concave stimuli in the picture plane.

Figure 6

Scheme for stimuli used in Experiment 2. Top row: the three different arm shapes that participants were instructed to identify. All three arm shapes are shown on the same (medium height) body shape for consistency of comparison. Bottom row: illustration of the orthogonal insertion manipulation of the irrelevant (body shape) dimension. During the pre-insertion block the body shape dimension did not vary; all stimuli had a medium height body. During the post-insertion block body shape changed randomly from trial to trial, uncorrelated with arm shape. All post-insertion examples shown with arm shape B for consistency of comparison.

Figure 7

Median reaction times for each bin of 20 trials, averaged across subjects for Experiment 2. The vertical line after trial 60 indicates the orthogonal insertion point dividing the pre- and post-insertion blocks. Error bars represent standard error of the mean.

Figure 8

The three types of distortion used to create foils in Experiment 3. The cross shape that served as the sample image for a trial (labeled “sample image” at top) has horizontal extent X and vertical extent Y. The same-area distortion elongated one dimension and shortened the other, which changed aspect ratio X/Y, but preserved the surface area of the shape (proportional to X*Y). The same-aspect-ratio distortion elongated the shape along both dimensions equally, which significantly increased surface area but preserved the shape’s aspect ratio. The one-axis distortion produced changes intermediate to these two extremes by stretching only one axis, changing both surface area and aspect ratio moderately. Note that the one-axis distortion is the only case that kept one of the shape’s original axis dimensions constant. All of the above examples show concave images and positive values of d; negative values of d were also used. The shapes’ square backgrounds have also been distorted for emphasis, although they were not distorted in the actual stimuli.

Figure 9

Top row: mean of individual subjects’ median RTs for Experiment 3. Error bars represent standard error of the mean. Bottom row: differences in modeled shape representations for the three distortion types, based on representing shapes by aspect ratio (left) by a city-block model in which differences were calculated by considering length and width as separable dimensions (right). Error bars represent standard deviations for the set of stimulus dimensions used in the trials of the experiment. Ordinates for the model data have been inverted so that small shape differences compare to higher RT in the behavioral data graphs.