Constraint-based probabilistic learning of metabolic pathways from tomato volatiles

Abstract

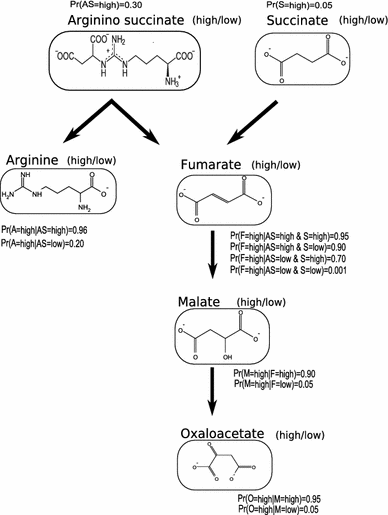
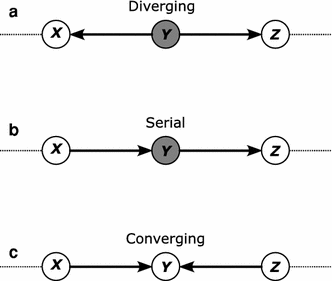
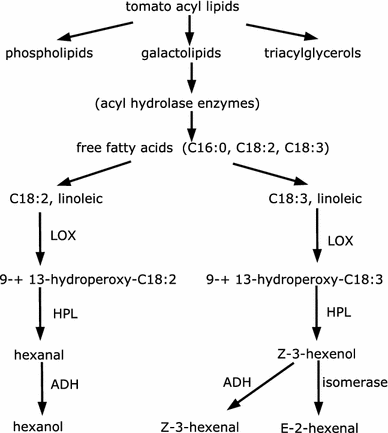
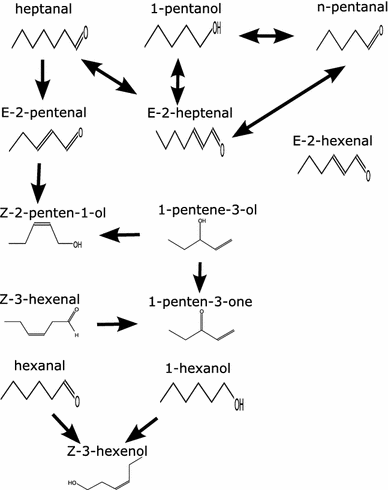
Clustering and correlation analysis techniques have become popular tools for the analysis of data produced by metabolomics experiments. The results obtained from these approaches provide an overview of the interactions between objects of interest. Often in these experiments, one is more interested in information about the nature of these relationships, e.g., cause-effect relationships, than in the actual strength of the interactions. Finding such relationships is of crucial importance as most biological processes can only be understood in this way. Bayesian networks allow representation of these cause-effect relationships among variables of interest in terms of whether and how they influence each other given that a third, possibly empty, group of variables is known. This technique also allows the incorporation of prior knowledge as established from the literature or from biologists. The representation as a directed graph of these relationship is highly intuitive and helps to understand these processes. This paper describes how constraint-based Bayesian networks can be applied to metabolomics data and can be used to uncover the important pathways which play a significant role in the ripening of fresh tomatoes. We also show here how this methods of reconstructing pathways is intuitive and performs better than classical techniques. Methods for learning Bayesian network models are powerful tools for the analysis of data of the magnitude as generated by metabolomics experiments. It allows one to model cause-effect relationships and helps in understanding the underlying processes. ELECTRONIC SUPPLEMENTARY MATERIAL: The online version of this article (doi:10.1007/s11306-009-0166-2) contains supplementary material, which is available to authorized users.

Fig. 1

Urea/Citric Acid cycle

Fig. 2

Example of a simple Bayesian network consisting of a probability distribution Pr and a directed graph. The probability distribution Pr is specified using conditional probability distribution associated to the individual nodes, such as Pr(A = high · AS = high) = 0.96

Fig. 3

Prior marginal probability distributions for the Bayesian belief network shown in Fig. 2

Fig. 4

Posterior marginal probability distributions for the Bayesian belief network after entering evidence on concentration levels of oxaloacetate. Note the increase in probabilities of the levels of concentrations of both oxaloacetate and argininosuccinate compared to Fig. 3. It also predicts that it is more likely that the %concentration levels of argininosuccinate to be high

Fig. 5

Three different graph structures of a Bayesian network and their interpretation

Fig. 6

Formation of lipid-derived volatiles through biosynthesis in the oxylipin pathway

Fig. 7

Constructed Bayesian network for 13 plant-derived compounds for beef, round and cherry tomatoes